题目内容
13. 如图(a) 所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,己知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图(b)所示.斜面倾角为37°,长为l,求:
如图(a) 所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,己知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图(b)所示.斜面倾角为37°,长为l,求:(1)滑块滑至斜面中点时的加速度大小;
(2)滑块滑至斜面底端时的速度大小.
分析 (1)根据牛顿第二定律求出滑块的加速度大小.
(2)根据动能定理求出滑块滑至斜面底端时的速度大小.
解答 解:(1)滑块滑到中点时,由(b)图可知,μ=0.5.
根据牛顿第二定律得:
mgsin37°-μmgcos37°=ma
解得:a=0.2g.
(2)滑块由顶端滑至底端,由动能定理得:$mglsin37°+{W}_{f}=\frac{1}{2}m{v}_{B}^{2}$
由图b的物理意义得:${W}_{f}=\overline{f}•l$
解得:${v}_{B}=\sqrt{0.4gl}$
答:(1)滑块滑至斜面中点时的加速度大小是0.2g;
(2)滑块滑至斜面底端时的速度大小是$\sqrt{0.4gl}$.
点评 本题综合考查了牛顿第二定律、动能定理等规律,综合性较强,对学生的能力要求较高,以及通过图象求出摩擦力做功是本题的难点.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
7.一个物体从H高处自由下落,以地面为零势能参考平面.当该物体的动能是其重力势能的两倍时,该物体离地面高为( )
| A. | $\frac{H}{3}$ | B. | $\frac{H}{2}$ | C. | $\frac{2H}{3}$ | D. | H |
1.下列说法正确的是( )
| A. | 光电效应既显示了光的粒子性,又显示了光的波动性 | |
| B. | 原子核内的中子转化成一个质子和一个电子,这种转化产生的电子发射到核外,就是β粒子,这就是β衰变的实质 | |
| C. | 一个氘核${\;}_{1}^{2}$H与一个氚核${\;}_{1}^{3}$H聚变生成一个氦核${\;}_{2}^{4}$He的同时,放出一个质子 | |
| D. | 光子的能量由光的频率所决定 | |
| E. | 按照玻尔理论,氢原子核外从半径较小的轨道跃迁半径较大的轨道时,电子的动能减小,电势能增大,原子的总能量增大 |
8. 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )| A. | 由此可知d电势高于c电势 | |
| B. | 由此可知Ⅰ是S极 | |
| C. | 由此可知Ⅰ是N极 | |
| D. | 当cd棒向下运动时,ab导线受到向左的磁场力 |
18.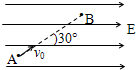 如图所示,在竖直面内一带电质点以速度v0沿图示方向射入水平向右的匀强电场中,结果质点沿直线运动到B点,到达B点时速度为0.此过程中重力势能和电势能的增量分别用△EG和△ED表示,粒子的质量用m表示,空气阻力不计.以下结论正确的是( )
如图所示,在竖直面内一带电质点以速度v0沿图示方向射入水平向右的匀强电场中,结果质点沿直线运动到B点,到达B点时速度为0.此过程中重力势能和电势能的增量分别用△EG和△ED表示,粒子的质量用m表示,空气阻力不计.以下结论正确的是( )
 如图所示,在竖直面内一带电质点以速度v0沿图示方向射入水平向右的匀强电场中,结果质点沿直线运动到B点,到达B点时速度为0.此过程中重力势能和电势能的增量分别用△EG和△ED表示,粒子的质量用m表示,空气阻力不计.以下结论正确的是( )
如图所示,在竖直面内一带电质点以速度v0沿图示方向射入水平向右的匀强电场中,结果质点沿直线运动到B点,到达B点时速度为0.此过程中重力势能和电势能的增量分别用△EG和△ED表示,粒子的质量用m表示,空气阻力不计.以下结论正确的是( )| A. | 质点一定带负电 | B. | 质点做的是匀变速运动 | ||
| C. | 质点受到的电场力小于其重力 | D. | △EG+△ED=$\frac{1}{2}$mv02 |
5.已知地球的半径为R,地球表面的重力加速度为g,环绕地球运行的一颗人造地球卫星的线速度为v,则下列说法正确的是( )
| A. | 地球的第一宇宙速度小于v | B. | 该卫星的轨道半径为$\frac{{v}^{2}}{g{R}^{2}}$ | ||
| C. | 该卫星的运行周期为2π$\frac{{gR}^{2}}{{v}^{3}}$ | D. | 该卫星的向心加速度为$\frac{{v}^{2}}{g{R}^{2}}$ |
2.下列关于电源电动势的说法,正确的是( )
| A. | 电动势表征的是电源将电能转化为其它形式能量的本领 | |
| B. | 外电路断开时的路端电压等于电源的电动势 | |
| C. | 电动势数值上等于闭合电路内外电压之和 | |
| D. | 外电路的总电阻越大,则路端电压越接近电源电动势 |
 如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )
如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )


