题目内容
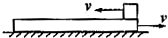
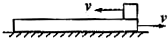
如图，质量为4kg的木板放在光滑水平面上，质量为1kg的物块放在木板上，它们之间有摩擦，木板足够长，最初两者都以4m/s的初速度向相反方向运动，当木板的速度为向右2.5m/s时，物块做（ ）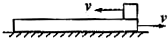
A．加速运动
B．减速运动
C．匀速运动
D．静止不动
【答案】分析：分析物体的运动情况：初态时，系统的总动量方向水平向左，两个物体开始均做匀减速运动，m的速度先减至零，根据动量守恒定律求出此时M的速度．之后，m向左做匀加速运动，M继续向左做匀减速运动，最后两者一起向左匀速运动．根据动量守恒定律求出薄板的速度大小为2.4m/s时，物块的速度，并分析m的运动情况．
解答：解：开始阶段，m向左减速，M向右减速，根据系统的动量守恒定律得：当m的速度为零时，设此时M的速度为v1．
根据动量守恒定律得 （M-m）v=Mv1
代入解得v1=23m/s．
此后m将向右加速，M继续向右减速；
当两者速度达到相同时，设共同速度为v2．
由动量守恒定律得 （M-m）v=（M+m）v2，
代入解得v2=2.4m/s．
两者相对静止后，一起向左匀速直线运动．
由此可知当M的速度为2.5m/s时，m处于向左加速过程中．
故选A．
点评：本题考查应用系统的动量守恒定律分析物体运动情况的能力，这是分析物体运动情况的一种方法，用得较少，但要学会，比牛顿定律分析物体运动情况简单．
解答：解：开始阶段，m向左减速，M向右减速，根据系统的动量守恒定律得：当m的速度为零时，设此时M的速度为v1．
根据动量守恒定律得 （M-m）v=Mv1
代入解得v1=23m/s．
此后m将向右加速，M继续向右减速；
当两者速度达到相同时，设共同速度为v2．
由动量守恒定律得 （M-m）v=（M+m）v2，
代入解得v2=2.4m/s．
两者相对静止后，一起向左匀速直线运动．
由此可知当M的速度为2.5m/s时，m处于向左加速过程中．
故选A．
点评：本题考查应用系统的动量守恒定律分析物体运动情况的能力，这是分析物体运动情况的一种方法，用得较少，但要学会，比牛顿定律分析物体运动情况简单．
练习册系列答案
相关题目
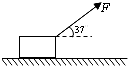如图，质量为4kg的物体静止于水平面上，物体与水平面间的动摩擦因数为0.5，物体在大小为20N、方向与水平方向成37°角斜向上的拉力F作用下，沿水平面做匀加速运动．（g取10m/s2，sin37°=0.6，cos37°=0.8）
（2007?淄博模拟）如图，质量为4kg的木板放在光滑水平面上，质量为1kg的物块放在木板上，它们之间有摩擦，木板足够长，最初两者都以4m/s的初速度向相反方向运动，当木板的速度为向右2.5m/s时，物块做（ ）
