Question

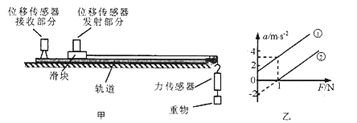
【题目】某实验小组设计了如图甲所示实验装置，探究滑块运动的加速度a和所受拉力F 的关系．在轨道水平和倾斜的两种情况下分别做了多组实验，将位移传感器和力传感器得到的多组数据输入计算机进行处理，得到了两条a-F图线①、②，如图乙所示．

(1)实验时，一定要进行的操作是______．

A．改变托盘中砝码的个数

B．滑块在轨道水平和倾斜的两种情况下必须在同一位置由静止释放

C．用天平测出托盘的质量

D．为减小误差，实验中一定要保证托盘和砝码的质量远小于滑块的质量

(2)在轨道倾斜的情况下得到的a-F图线是____．（选填①或②）

(3)滑块和位移传感器发射部分的总质量m=______kg;滑块和轨道间的动摩擦因数= ___（重力加速度g取10 ）

Answer 1

【答案】 A; ①; 0.5; 0.2;

【解析】(1)A项：由于探究加速度与合外力的关系，所以应改变物块的合外力，即改变托盘中砝码的个数，故A正确；

B项：滑块的释放位置对该实验没有影响，不要求每次在同一位置，故B错误；

C、D项：本题拉力可以由力的传感器测出，不需要用天平测出砂和砂桶的质量，也就不需要使小桶（包括砂）的质量远小于车的总质量，故C错误，D错误；

(2) 由图象可知，当F=0时，a≠0．也就是说当绳子上没有拉力时小车就有加速度，该同学实验操作中平衡摩擦力过大，即倾角过大，平衡摩擦力时木板的右端垫得过高，

所以图线①是在轨道右侧抬高成为斜面情况下得到的；

(3) 所以滑块运动的加速度a和所受拉力F的关系图象斜率等于滑块和位移传感器发射部分的总质量的倒数，由图形b得加速度a和所受拉力F的关系图象斜率k=2，所以滑块和位移传感器发射部分的总质量m=0.5Kg

由图形b得，在水平轨道上F=1N时，加速度a=0，

根据牛顿第二定律得F-μmg=0

解得μ=0.2

点晴：通过作出两个量的图象，然后由图象去寻求未知量与已知量的关系．运用数学知识和物理量之间关系式结合起来求解。