题目内容
5. 如图所示,在动摩擦因数μ=0.2的水平面上有一质量m=lkg的小球,一水平放置的轻弹簧一端与墙相连,另一端与小球相连,一不可伸长的轻质细绳一端与小球相连,另一端固定在天花板上,细绳与竖直方向成45°角,此时小球处于静止状态,且水平面对小球的弹力恰好为零.取g=10m/s2,小球所受的最大静摩擦力等于滑动摩擦力,则在烧断轻绳的瞬间,下列说法正确的是( )
如图所示,在动摩擦因数μ=0.2的水平面上有一质量m=lkg的小球,一水平放置的轻弹簧一端与墙相连,另一端与小球相连,一不可伸长的轻质细绳一端与小球相连,另一端固定在天花板上,细绳与竖直方向成45°角,此时小球处于静止状态,且水平面对小球的弹力恰好为零.取g=10m/s2,小球所受的最大静摩擦力等于滑动摩擦力,则在烧断轻绳的瞬间,下列说法正确的是( )| A. | 小球所受合外力为零 | |
| B. | 弹簧的弹力大小为$10\sqrt{2}$N | |
| C. | 小球的加速度大小为10m/s2,方向向左 | |
| D. | 小球的加速度大小为8m/s2,方向向左 |
分析 先分析剪断轻绳前弹簧的弹力和轻绳的拉力大小,再研究剪断轻绳瞬间,抓住弹簧的弹力没有变化,求解小球的合力,由牛顿第二定律求出小球的加速度和水平面对小球的支持力.
解答 解:剪断轻绳前小球受力情况,如图所示,根据平衡条件得:
轻弹簧的弹力大小为:F=mg=10N,
细线的拉力大小为:T=$\sqrt{2}$mg=10$\sqrt{2}$N
剪断轻绳瞬间弹簧的弹力没有变化,此时轻弹簧的弹力大小仍为F=10N,所以小球合力为F=10N,方向水平向左,
小球所受的最大静摩擦力为:f=μmg=0.2×10N=2N,根据牛顿第二定律得小球的加速度为:
a=$\frac{F-f}{m}=\frac{10-2}{1}m/{s}^{2}=8m/{s}^{2}$,方向水平向左;
故选:D.
点评 本题是瞬时问题,先分析剪断轻绳前小球的受力情况,再分析剪断轻绳瞬间的受力情况,再根据牛顿第二定律求解瞬间的加速度.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
15.把甲物体从2h高处以速度V水平抛出,落地点的水平距离为L,把乙物体从h高处以速度2v水平抛出,落地点的水平距离为S,比较L与S,可知( )
| A. | L=$\frac{S}{2}$ | B. | L=2S | C. | L=$\frac{1}{{\sqrt{2}}}$S | D. | L=$\sqrt{2}$S |
13. 野营活动中,学生在平地上用三根轻质斜杆搭建一个正三棱锥形的三脚支架P-ABC进行野炊训练.己知PC=60cm,A.B两点间距离为36$\sqrt{3}$cm,若锅及锅中所盛食物的总质量为3kg,g取10m/s2.则每根斜杆承受的力为( )
野营活动中,学生在平地上用三根轻质斜杆搭建一个正三棱锥形的三脚支架P-ABC进行野炊训练.己知PC=60cm,A.B两点间距离为36$\sqrt{3}$cm,若锅及锅中所盛食物的总质量为3kg,g取10m/s2.则每根斜杆承受的力为( )
 野营活动中,学生在平地上用三根轻质斜杆搭建一个正三棱锥形的三脚支架P-ABC进行野炊训练.己知PC=60cm,A.B两点间距离为36$\sqrt{3}$cm,若锅及锅中所盛食物的总质量为3kg,g取10m/s2.则每根斜杆承受的力为( )
野营活动中,学生在平地上用三根轻质斜杆搭建一个正三棱锥形的三脚支架P-ABC进行野炊训练.己知PC=60cm,A.B两点间距离为36$\sqrt{3}$cm,若锅及锅中所盛食物的总质量为3kg,g取10m/s2.则每根斜杆承受的力为( )| A. | $\frac{20\sqrt{3}}{3}$N | B. | 12.5N | C. | 10$\sqrt{2}$N | D. | 20N |
10.关于等势面正确的说法是( )
| A. | 电荷在等势面上移动时不受电场力作用,所以不做功 | |
| B. | 等势面上各点的场强大小相等 | |
| C. | 等势面一定跟电场线垂直 | |
| D. | 两数值不等的等势面永不相交 |
17.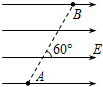 如右图所示,在匀强电场中,将一电荷量为q的正电荷由A点移到B点,电场力做功为W,已知A、B两点间距离为L,两点连线与电场方向成60°角,则该匀强电场的电场强度为( )
如右图所示,在匀强电场中,将一电荷量为q的正电荷由A点移到B点,电场力做功为W,已知A、B两点间距离为L,两点连线与电场方向成60°角,则该匀强电场的电场强度为( )
 如右图所示,在匀强电场中,将一电荷量为q的正电荷由A点移到B点,电场力做功为W,已知A、B两点间距离为L,两点连线与电场方向成60°角,则该匀强电场的电场强度为( )
如右图所示,在匀强电场中,将一电荷量为q的正电荷由A点移到B点,电场力做功为W,已知A、B两点间距离为L,两点连线与电场方向成60°角,则该匀强电场的电场强度为( )| A. | $\frac{2W}{qL}$ | B. | $\frac{W}{2qL}$ | C. | $\frac{{2\sqrt{3}W}}{3qL}$ | D. | $\frac{W}{qL}$ |
15.关于重心的叙述,不正确的是( )
| A. | 只有物体的重心处才受重力作用 | |
| B. | 质量分布均匀的圆柱体的重心在其轴线的中点 | |
| C. | 物体的重心位置跟物体的质量分布情况和物体的形状有关 | |
| D. | 用线悬挂的静止物体,细线方向一定通过物体的重心 |