题目内容
 (2011?泰州一模)如图所示,x0y平面内,y轴左侧有方向竖直向下,电场强度为E=1.0×104N/的匀强电场.在Y轴右侧有一个边界为圆形的匀强磁场区域,圆心O′位于x轴上,半径为r=0.01m,磁场最左边与Y轴相切于O点,磁感应强度为B=0.01T,方向垂直纸面向里.在坐标xo=0.06m处有垂直于x轴的足够大的荧光屏PQ.一束带正电的粒子从电场中的A点(图中未标出)以垂直于电场的初速度向右运动,穿出电场时恰好通过坐标原点,速度大小为v=2×106m/s,方向与x轴正向成300角斜向下.已知粒子的质量为m=1.0×l0-2kg,电量为q=1.0×10-10C,重力不计.
(2011?泰州一模)如图所示,x0y平面内,y轴左侧有方向竖直向下,电场强度为E=1.0×104N/的匀强电场.在Y轴右侧有一个边界为圆形的匀强磁场区域,圆心O′位于x轴上,半径为r=0.01m,磁场最左边与Y轴相切于O点,磁感应强度为B=0.01T,方向垂直纸面向里.在坐标xo=0.06m处有垂直于x轴的足够大的荧光屏PQ.一束带正电的粒子从电场中的A点(图中未标出)以垂直于电场的初速度向右运动,穿出电场时恰好通过坐标原点,速度大小为v=2×106m/s,方向与x轴正向成300角斜向下.已知粒子的质量为m=1.0×l0-2kg,电量为q=1.0×10-10C,重力不计.(1)求粒子出发点A的坐标;
(2)若圆形磁场可沿x轴向右移动,圆心O仍在x轴上,由于磁场位置的不同,导致该粒子打在荧光屏上的位置也不同,求粒子打在荧光屏上的位置范围;
(3)若改变磁场半径,磁场最左边仍然与Y轴相切于O点,当磁场半径至少为多大时,粒子就再也不能打到带屏上?
分析:(1)粒子沿AB方向进入电场后做类平抛运动,将射出电场的速度进行分解,根据沿电场方向上的速度,结合牛顿第二定律求出运动的时间,从而得出类平抛运动的水平位移和竖直位移,即得出射入电场的坐标.
(2)随着磁场向右移动荧光屏光点位置逐渐下移,当v方向与磁场圆形区域相切,此后,粒子将打在荧光屏的同一位置.根据粒子在匀强磁场中的半径公式,结合几何关系求出粒子打在荧光屏上的范围.
(3)当粒子射出磁场时的速度平行于y轴时,将不再打到荧光屏上,有几何关系即可求解.
(2)随着磁场向右移动荧光屏光点位置逐渐下移,当v方向与磁场圆形区域相切,此后,粒子将打在荧光屏的同一位置.根据粒子在匀强磁场中的半径公式,结合几何关系求出粒子打在荧光屏上的范围.
(3)当粒子射出磁场时的速度平行于y轴时,将不再打到荧光屏上,有几何关系即可求解.
解答: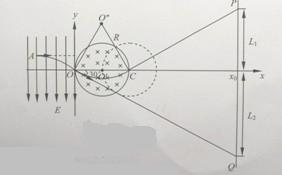 解:(1)粒子沿AB方向进入电场后做类平抛运动,在O点将v沿x、y方向分解得:
解:(1)粒子沿AB方向进入电场后做类平抛运动,在O点将v沿x、y方向分解得:
vx=vcos30°=
×106m/s.
vy=vsin30°=1×106m/s
根据牛顿第二定律a=
=1×1014m/s2.
粒子从射入到0点的时间为:
t=
=
s=1×10-8s
粒子刚射入电场时A点的坐标分别为:
x=-vxt=-
×10-2m
y=
vyt=5×10-3m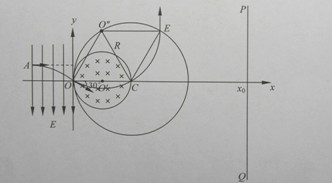
即粒子出发点A的坐标为(-
×10-2m,5×10-3m)
(2)洛仑兹力提供向心力,则qvB=m
,解得:R=
=0.02m=2r
由几何关系可知,粒子射出磁场的位置为C点,轨迹如图所示:
则粒子打在荧光屏最高点到x轴的距离为:l1=(x0-2r)tan30°=2.31×10-2m
随着磁场向右移动荧光屏光点位置逐渐下移,当v方向与磁场圆形区域相切,粒子打在荧光屏的最低点,此后,粒子将打在荧光屏的同一位置.
其最低到x轴的距离为:x0tan30°=3.46×10-2m
(3)如图所示,当粒子射出磁场时的速度平行于y轴时,将不再打到荧光屏上,OCE0″为菱形,
由几何关系得:
磁场半径至少为r=R=0.02m
答:(1)粒子出发点A的坐标为(-
×10-2m,5×10-3m);
(2)粒子打在荧光屏上的位置范围为[2.31×10-2m,3.46×10-2m];
(3)当磁场半径至少为0.02m时,粒子就再也不能打到带屏上.
 解:(1)粒子沿AB方向进入电场后做类平抛运动,在O点将v沿x、y方向分解得:
解:(1)粒子沿AB方向进入电场后做类平抛运动,在O点将v沿x、y方向分解得:vx=vcos30°=
| 3 |
vy=vsin30°=1×106m/s
根据牛顿第二定律a=
| qE |
| m |
粒子从射入到0点的时间为:
t=
| vy |
| a |
| 1×106 |
| 1×1014 |
粒子刚射入电场时A点的坐标分别为:
x=-vxt=-
| 3 |
y=
| 1 |
| 2 |

即粒子出发点A的坐标为(-
| 3 |
(2)洛仑兹力提供向心力,则qvB=m
| v2 |
| R |
| mv |
| Bq |
由几何关系可知,粒子射出磁场的位置为C点,轨迹如图所示:
则粒子打在荧光屏最高点到x轴的距离为:l1=(x0-2r)tan30°=2.31×10-2m
随着磁场向右移动荧光屏光点位置逐渐下移,当v方向与磁场圆形区域相切,粒子打在荧光屏的最低点,此后,粒子将打在荧光屏的同一位置.
其最低到x轴的距离为:x0tan30°=3.46×10-2m
(3)如图所示,当粒子射出磁场时的速度平行于y轴时,将不再打到荧光屏上,OCE0″为菱形,
由几何关系得:
磁场半径至少为r=R=0.02m
答:(1)粒子出发点A的坐标为(-
| 3 |
(2)粒子打在荧光屏上的位置范围为[2.31×10-2m,3.46×10-2m];
(3)当磁场半径至少为0.02m时,粒子就再也不能打到带屏上.
点评:本题考查粒子在电场中类平抛运动和在磁场中的匀速圆周运动,对学生几何能力要求较高,能够找出问题的临界情况是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?泰州一模)点电荷A、B是带电量为Q的正电荷,C、D是带电量为Q的负电荷,它们处在一个矩形的四个顶点上.它们产生静电场的等势面如图中虚线所示,在电场中对称地有一个正方形路径abcd(与ABCD共面),如图中实线所示,O为正方形与矩形的中心,则( )
(2011?泰州一模)点电荷A、B是带电量为Q的正电荷,C、D是带电量为Q的负电荷,它们处在一个矩形的四个顶点上.它们产生静电场的等势面如图中虚线所示,在电场中对称地有一个正方形路径abcd(与ABCD共面),如图中实线所示,O为正方形与矩形的中心,则( ) 图所示.开始时使弹簧伸长,放开物块后物块沿斜面向上运动,然后上滑到最高点,在此过程中,M保持静止状态,则地面对M的摩擦力( )
图所示.开始时使弹簧伸长,放开物块后物块沿斜面向上运动,然后上滑到最高点,在此过程中,M保持静止状态,则地面对M的摩擦力( ) (2011?泰州一模)如图所示,用三条细线悬挂的金属圆环,金属环粗细均匀、单位长度的质量为2.5g,三条细线呈对称分布,稳定时金属环面水平,在金属环正下方放有一个圆柱形磁铁,磁铁的中轴线OO′垂直于金属环面且通过其圆心O,测得金属环所在处磁感应强度大小为0.5T,与竖直方向成30°角.现在要使金属环各部分所受安培力的合力竖直向上且恰好等于其自身的重力,则在金属环中通过的电流大小至少为( )(取g=10m/s2)
(2011?泰州一模)如图所示,用三条细线悬挂的金属圆环,金属环粗细均匀、单位长度的质量为2.5g,三条细线呈对称分布,稳定时金属环面水平,在金属环正下方放有一个圆柱形磁铁,磁铁的中轴线OO′垂直于金属环面且通过其圆心O,测得金属环所在处磁感应强度大小为0.5T,与竖直方向成30°角.现在要使金属环各部分所受安培力的合力竖直向上且恰好等于其自身的重力,则在金属环中通过的电流大小至少为( )(取g=10m/s2) (2011?泰州一模)如图所示,Dl、D2规格相同的两个小灯泡,L是带有铁芯的电阻忽略不计的电感线圈,下列说法正确的是( )
(2011?泰州一模)如图所示,Dl、D2规格相同的两个小灯泡,L是带有铁芯的电阻忽略不计的电感线圈,下列说法正确的是( )