题目内容
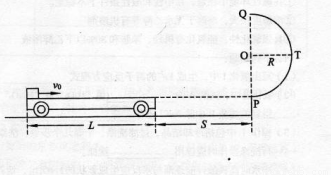
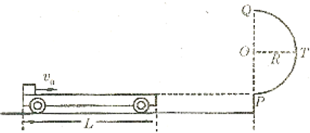
如图所示，地面和半圆轨道面PTQ均光滑．质量M=lkg的小车放在地面上，小车上表面与半圆轨道最低点P的切线相平．现有一质量m=2kg的滑块（不计大小）以υ0=6m/s的初速度滑上小车左端，带动小车向右运动，小车跟墙壁碰撞时，滑块处在小车正中间位置且恰好与小车达到共同速度，碰后小车即被粘在墙壁上，滑块最终通过了半圆形轨道的最高点，已知滑块与小车表面的动摩擦因数片μ=0.2，g取10m/s2求：
（1）小车的长度L；
（2）圆轨道半径R的取值范围．
（1）小车的长度L；
（2）圆轨道半径R的取值范围．
分析：（1）对滑块和小车进行受力分析，运用牛顿第二定律和运动学公式求解
（2）滑块恰好通过最高点，由牛顿第二定律求得临界速度，由动能定理研究滑块从小车与墙壁碰撞到最高点求解
（2）滑块恰好通过最高点，由牛顿第二定律求得临界速度，由动能定理研究滑块从小车与墙壁碰撞到最高点求解
解答：解：（1）对滑块和小车进行受力分析，运用牛顿第二定律和运动学公式得
对滑块μmg=ma1
ν=ν0-a1t
x1=
t
对小车μmg=Ma2
ν=a2t
x2=
t
又
=x1-x2
由以上各式解得L=6m
（2）由动能定理研究滑块从小车与墙壁碰撞到最高点得
mνQ2-
mv2=-μmg
-2mgR
若滑块恰好通过最高点，由牛顿第二定律得mg=m
解得R=0.08m
所以半径的取值范围为R≤0.08m
答：（1）小车的长度是6m；
（2）圆轨道半径R的取值范围是R≤0.08m．
对滑块μmg=ma1
ν=ν0-a1t
x1=
| ν+ν0 |
| 2 |
对小车μmg=Ma2
ν=a2t
x2=
| ν |
| 2 |
又
| L |
| 2 |
由以上各式解得L=6m
（2）由动能定理研究滑块从小车与墙壁碰撞到最高点得
| 1 |
| 2 |
| 1 |
| 2 |
| L |
| 2 |
若滑块恰好通过最高点，由牛顿第二定律得mg=m
| vQ2 |
| R |
解得R=0.08m
所以半径的取值范围为R≤0.08m
答：（1）小车的长度是6m；
（2）圆轨道半径R的取值范围是R≤0.08m．
点评：考查了牛顿第二定律和运动学公式的应用，第2题要考虑滑块通过最高点的情况，要培养自己分析隐含的临界状态的能力．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，地面和半圆轨道面PTQ均光滑．质量M=1kg、长L=4m的小车放在地面上，右端与墙壁的距离为S=3m，小车上表面与半圆轨道最低点P的切线相平．现有一质量m=2kg的滑块（不计大小）以vo=6m/s的初速度滑上小车左端，带动小车向右运动．小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数μ=0.2，g取10m/S2．求：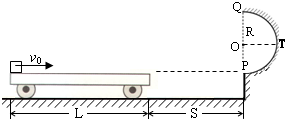
如图所示，地面和半圆轨道面均光滑，质量M=1kg、长L=4m的小车放在地面上，其右端与墙壁的距离S=3m，小车上表面与半圆轨道最低点P的切线相平．现有一质量m=2kg的滑块（可视为质点）以v0=6m/s的初速度滑上小车左端，带动小车向右运动，小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数μ=0.2，g取10m/s2．
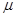=0.2，g取m/s2。