题目内容
如图所示,一带电微粒,从A点射入水平方向的匀强电场中(实线代表电场线,电场方向未知),微粒恰沿直线AB运动,AB与水平方向夹角θ = 30°,已知带电微粒的质量m = 1.0×10-7 kg,电荷量q = 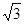 ×10-10C,A与B相距L =" 40" cm,取g =" 10" m/s2。则下列说法正确的是
×10-10C,A与B相距L =" 40" cm,取g =" 10" m/s2。则下列说法正确的是

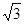 ×10-10C,A与B相距L =" 40" cm,取g =" 10" m/s2。则下列说法正确的是
×10-10C,A与B相距L =" 40" cm,取g =" 10" m/s2。则下列说法正确的是
| A.微粒一定带负电 |
| B.微粒可能始终做匀加速直线运动 |
| C.AB两点间电势差的大小为2.0×103 V |
| D.要使微粒能从A点运动到B点,微粒射入电场时的速度至少为4 m/s |
D
根据直线运动的条件并结合受力分析,得到电场力的方向,最终分析出物体的运动规律;根据力的合成的平行四边形定则并结合几何关系得到电场力;对粒子的运动过程运用动能定理列式求解即可.
解:微粒只在重力和电场力作用下沿AB直线运动,故合力一定与速度在同一条直线上,如图所示.微粒所受合力的方向由B指向A,与初速度VA方向相反,微粒做匀减速直线运
动.即微粒做匀减速直线运动.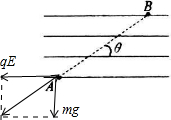
根据共点力平衡条件,有:qE=mgtanθ
故电场强度E=1.7×104N/C,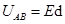
微粒由A运动到B的速度vB=0,微粒进入电场中的速度最小,由动能定理有:
mgLsinθ+qELcosθ=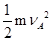 解得vA=4m/s
解得vA=4m/s
即要使微粒从A点运动到B点,微粒射入电场时的最小速度是2.8m/s.
解:微粒只在重力和电场力作用下沿AB直线运动,故合力一定与速度在同一条直线上,如图所示.微粒所受合力的方向由B指向A,与初速度VA方向相反,微粒做匀减速直线运
动.即微粒做匀减速直线运动.

根据共点力平衡条件,有:qE=mgtanθ
故电场强度E=1.7×104N/C,
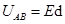
微粒由A运动到B的速度vB=0,微粒进入电场中的速度最小,由动能定理有:
mgLsinθ+qELcosθ=
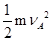 解得vA=4m/s
解得vA=4m/s即要使微粒从A点运动到B点,微粒射入电场时的最小速度是2.8m/s.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

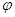 A、
A、

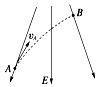
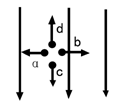
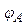 、
、 、
、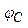 ,关于这三点的电场强度和电势的关系,以下判断正确的是( )
,关于这三点的电场强度和电势的关系,以下判断正确的是( )