题目内容
3. 北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )
北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )| A. | 在轨道Ⅰ上运动到P点的速度比在轨道Ⅱ上运动到P点的速度小 | |
| B. | 在轨道Ⅰ上运行的速率为$\sqrt{{g}_{0}R}$ | |
| C. | 在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大 | |
| D. | 在轨道Ⅰ上运动的周期小于在轨道Ⅱ上运动的周期 |
分析 当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动,若是万有引力大于需要的向心力,则卫星做逐渐靠近圆心的运动;若是万有引力小于需要的向心力,则卫星做逐渐远离圆心的运动;根据开普勒周期定律比较两个轨道上的周期.
解答 解:A、在轨道Ⅰ上到达P点要刹车制动才能成功变轨到椭圆轨道Ⅱ,故在轨道Ⅰ上运动到P点的速度比在轨道Ⅱ上运动到P点的速度大,故A错误;
B、在轨道Ⅰ运动时,万有引力提供向心力,故:
G$\frac{Mm}{{(3R+R)}^{2}}$=m$\frac{{v}^{2}}{3R+R}$
在月球表面,重力等于万有引力,故:
$G\frac{Mm}{{R}^{2}}=m{g}_{0}$
联立解得:
v=$\frac{1}{2}\sqrt{{g}_{0}R}$
故B错误;
C、变轨的时候飞船需要点火,发动机做功,从轨道Ⅰ进入轨道Ⅱ,发动机要做功使卫星减速,故在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大,故C正确;
D、根据开普勒第三定律$\frac{{a}^{3}}{{T}^{2}}=k$,k为常数,可得半长轴a越大,运动周期越大,显然轨道Ⅰ的半长轴(半径)大于轨道Ⅱ的半长轴,故沿轨道Ⅱ运动的周期小于沿轨道?运动的周期,故D错误;
故选:C
点评 本题关键是记住:由高轨道变轨到低轨道需要减速,而由低轨道变轨到高轨道需要加速;同时要结合在星球表面重力等于万有引力,卫星的万有引力提供向心力列式.

练习册系列答案
相关题目
18.关于空气湿度和热力学定律,下列说法正确的是 ( )
| A. | 热量可能会自发地从低温物体传向高温物体 | |
| B. | 功转变为热的实际宏观过程是可逆过程 | |
| C. | 空气的绝对湿度用空气中所含水蒸气的质量表示 | |
| D. | 无论、在冬季还是在夏季,当人们的皮肤感到干燥时,空气相对湿度一定较小 |
8.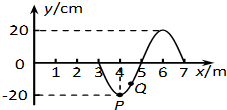 t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是 ( )
t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是 ( )
 t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是 ( )
t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是 ( )| A. | 周期为2s | |
| B. | 0~4s时间内质点P运动的总路程为80m | |
| C. | t=0时刻波源的振动方向沿y轴负方向 | |
| D. | t=7s时刻质点P位于波峰 | |
| E. | t=6.5s时刻开始质点Q比质点P第一次先回到平衡位置 |
13.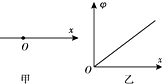 如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子仅受电场力的作用,则( )
如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子仅受电场力的作用,则( )
 如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子仅受电场力的作用,则( )
如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子仅受电场力的作用,则( )| A. | 电场一定是匀强电场 | B. | 电场的场强沿Ox方向增大 | ||
| C. | 电子将沿Ox负方向运动 | D. | 电子的电势能将增大 |
 如图所示,在光滑的水平面上有一质量为mA=0.5kg的木块A,现有质量为mB=0.1kg的小物块B以初速度v0=30m/s水平速度滑上A表面,由于B与A间有摩擦且A、B间的动摩擦因数为μ=0.2,B最终恰好在木块A的上表面右端边缘处相对A静止.求:
如图所示,在光滑的水平面上有一质量为mA=0.5kg的木块A,现有质量为mB=0.1kg的小物块B以初速度v0=30m/s水平速度滑上A表面,由于B与A间有摩擦且A、B间的动摩擦因数为μ=0.2,B最终恰好在木块A的上表面右端边缘处相对A静止.求:
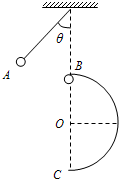 如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到悬点正下方B处线被拉断,紧接着摆球恰好能沿竖直放置的半圆形轨道内侧做圆周运动,已知摆线长l=2.0m,轨道半径R=2.0m,摆球质量m=0.5kg,不计空气阻力.(g取10m/s2)
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到悬点正下方B处线被拉断,紧接着摆球恰好能沿竖直放置的半圆形轨道内侧做圆周运动,已知摆线长l=2.0m,轨道半径R=2.0m,摆球质量m=0.5kg,不计空气阻力.(g取10m/s2) 武汉的许多餐厅生意火爆,能为服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处.某服务员用手托托盘方式(如图)给10m远处顾客上菜,要求全程托盘水平.托盘和手、碗之间的摩擦因数分别为0.2、0.125,服务员上菜最大速度为2.5m/s,g=10m/s2,可认为最大静摩擦力等于滑板摩擦力.
武汉的许多餐厅生意火爆,能为服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处.某服务员用手托托盘方式(如图)给10m远处顾客上菜,要求全程托盘水平.托盘和手、碗之间的摩擦因数分别为0.2、0.125,服务员上菜最大速度为2.5m/s,g=10m/s2,可认为最大静摩擦力等于滑板摩擦力.