题目内容
一水平传送带以1m／s的速度逆时针转动，水平部分AB长为2m，其右端与一倾角θ=37°的斜面平滑相连，一个可视为质点的物块从斜面上距斜面底端B点1m处无初速度释放，物块与斜面及传送带间动摩擦因数μ=0.5，问：(sin37°=0．6，g取l0m／s2)
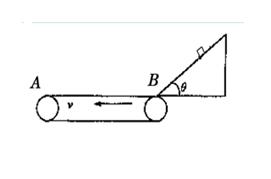
小题1:物块滑到斜面底端B的速度大小；
小题2:物块从释放至到达传送带左端A所用的时间.
小题1:物块滑到斜面底端B的速度大小；
小题2:物块从释放至到达传送带左端A所用的时间.
小题1:v1=2m/s
小题2:2.9s
(1)物块在斜面上无初速下滑过程，加速度为a1,
由牛顿第二定律：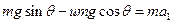
（1分）
到达斜面底端的速度为v1,v12=2a1s
解得：v1="2m/s " （1分）
到达斜面底端用时t1, v1=a1 t1
解得：t1="1s " （1分）
设物块在传送带上匀减速到与传送带同速过程，加速度为a2，对地位移为s2,用时t2
-umg=ma2 （1分）
v2-v12=2a2s2 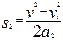（1分）
（1分）
减速运动时间为t2, v=v1+a2t2 t2="0.2s " （1分）
此后物块匀速运动至左端，用时t3 vt3=L-s2
解得： t3="1.7s " （1分）
运动至左端用时t=t1+t2+t3="2.9s " （1分）
由牛顿第二定律：
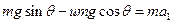（1分）到达斜面底端的速度为v1,v12=2a1s
解得：v1="2m/s " （1分）
到达斜面底端用时t1, v1=a1 t1
解得：t1="1s " （1分）
设物块在传送带上匀减速到与传送带同速过程，加速度为a2，对地位移为s2,用时t2
-umg=ma2 （1分）
v2-v12=2a2s2 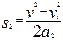（1分）
（1分）减速运动时间为t2, v=v1+a2t2 t2="0.2s " （1分）
此后物块匀速运动至左端，用时t3 vt3=L-s2
解得： t3="1.7s " （1分）
运动至左端用时t=t1+t2+t3="2.9s " （1分）
练习册系列答案
相关题目
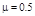，运动员滑到斜面底端时仅速度方向变为水平，大小不变。忽略空气阻力，重力加速度g=10m/s2。（sin37°=0.6；cos37°=0.8），求：
