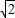题目内容
一物体沿长为l的光滑斜面,从静止开始由斜面的顶端下滑到底端的过程做匀加速运动,当物体的速度达到末速度的一半时,它沿斜面下滑的长度为( )
分析:物体沿光滑斜面,从静止开始由斜面的顶端下滑到底端的过程是匀加速运动,所以中间时刻的瞬时速度等于全程的平均速度,应用匀变速运动规律列式求解.
解答:解:设末速度为v,全程用时为t
则:l=
t=
t ①
中间时刻的瞬时速度等于全程的平均速度
所以当v1=
是用时t1=
所以此时的位移:x=
t1=
×
=
t②
由①②联立得:
=
=
故选A
此题也可以应用初速度为零的匀变速直线运动在1t内,2t内,3t内…位移之比为1:4:9…:n2求解
则:l=
. |
| v |
| 0+v |
| 2 |
中间时刻的瞬时速度等于全程的平均速度
所以当v1=
| v |
| 2 |
| t |
| 2 |
所以此时的位移:x=
. |
| v |
0+
| ||
| 2 |
| t |
| 2 |
| v |
| 8 |
由①②联立得:
| x |
| l |
| ||
|
| 1 |
| 4 |
故选A
此题也可以应用初速度为零的匀变速直线运动在1t内,2t内,3t内…位移之比为1:4:9…:n2求解
点评:此题为匀变速直线运动规律的应用,关键点在当物体的速度达到末速度的一半时,用时为全程用时的一半,找准这个关系列式求解即可,方法可以有很多种,可分别试试.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -1) C.L/2D.L/
-1) C.L/2D.L/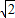 -1)
-1)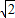
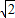 -1)
-1)