题目内容
（18分）一个质量为
的小球被长为L的轻质细绳悬挂，小球可以绕悬点O在竖直平面内摆动，不计空气阻力，则开始小球静止且恰能与地面接触而不发生相互作用，一个质量为
的小物块在光滑水平面上滑行并与小球发生正碰，碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动，当小球再次与物块发生正碰后，小物块速度变为最初速度的一半，已知重力加速度为
，两物体均可视为质点，试求
1.小物块最初的速度V0的大小；
2.第二次碰撞中系统损失的机械能
。
1.小球恰好通过最高点作圆周运动，此时重力刚好提供向心力，设速度为V，有
（3分）
得V=
设小球第一次碰完后速度为V1，其后在摆至最高点过程中，根据动能定理：
-2·2mgL=
·2m V2-·2m V12 （3分）
代入V值可得V1=
第一次碰撞过程中，物块和小球系统动量守恒，有
mV0=2m V1
代入V1值可得V0=2 （3分）
2.小球从第一次碰后到第二次碰前，由于机械能守恒且同在最低点，所以第二次碰前的速度仍为V1。
设小球第二次碰完后的速度为V2，根据第二次碰撞物块和小球系统动量守恒
2m V1=2m V2+m˙V0 （2分）
代入V1、V0值可得V2= （2分）
故第二次碰撞系统损失的机械能
ΔE=·2m V12-·2m V22-m（V0）2 （3分）
代入所求的的速度值可得
ΔE=
mgL （2分）
解析:略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
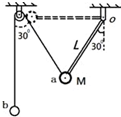如图所示，小球a被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点，同时又通过绳跨过光滑定滑轮与另一个质量为m小球b相连，整个装置平衡时杆和绳与竖直方向的夹角均为30°．若将小球a拉水平位置（杆呈水平状态）开始释放，不计摩擦，竖直绳足够长，求：
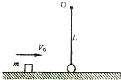一个质量为2m的小球被长为L的轻质细绳悬挂，小球可以绕悬点O在竖直平面内摆动，不计空气阻力，则开始小球静止且恰能与地面接触而不发生相互作用，一个质量为m的小物块在光滑水平面上滑行并与小球发生正碰，碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动，当小球再次与物块发生正碰后，小物块速度变为最初速度的一半，已知重力加速度为g，两物体均可视为质点，试求
的小球被长为L的轻质细绳悬挂，小球可以绕悬点O在竖直平面内摆动，不计空气阻力，则开始小球静止且恰能与地面接触而不发生相互作用，一个质量为
的小物块在光滑水平面上滑行并与小球发生正碰，碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动，当小球再次与物块发生正碰后，小物块速度变为最初速度的一半，已知重力加速度为
，两物体均可视为质点，试求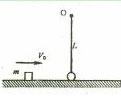
。
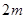的小球被长为L的轻质细绳悬挂，小球可以绕悬点O在竖直平面内摆动，不计空气阻力，则开始小球静止且恰能与地面接触而不发生相互作用，一个质量为
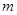的小物块在光滑水平面上滑行并与小球发生正碰，碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动，当小球再次与物块发生正碰后，小物块速度变为最初速度的一半，已知重力加速度为
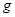，两物体均可视为质点，试求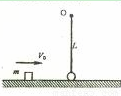
。
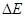