题目内容
 如图所示,物块重100N,放置在倾角为30°的斜面上,物块与斜面间的动摩擦因数为
如图所示,物块重100N,放置在倾角为30°的斜面上,物块与斜面间的动摩擦因数为| 1 | 3 |
分析:根据受力分析,结合力的平行四边形定则,运用数学知识,即可求解.
解答: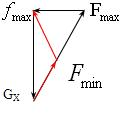 解:先将物体的重力分解为平行于斜面的力GX和与斜面垂直的力GY,
解:先将物体的重力分解为平行于斜面的力GX和与斜面垂直的力GY,
且有方向不变大小可变GX=G?sin30°=
,
GY=G?cos30°,
显然GX与N平衡,而平行斜面内三力平衡.则GX、F、f三力组成一个封闭三角形,
该三角形中,GX、大小、方向均不变,F的方向不变大小可变,f的大小、方向均可变,
但有f≤fmax
而最大静摩擦力fmax=μN=
G,
右图中,余弦定理得:
=
+F2-2GxFcos30°
解得:FMIN=28.8N;
FMAX=57.7N,
因此28.8N≤F≤57.7N
 解:先将物体的重力分解为平行于斜面的力GX和与斜面垂直的力GY,
解:先将物体的重力分解为平行于斜面的力GX和与斜面垂直的力GY,且有方向不变大小可变GX=G?sin30°=
| G |
| 2 |
GY=G?cos30°,
显然GX与N平衡,而平行斜面内三力平衡.则GX、F、f三力组成一个封闭三角形,
该三角形中,GX、大小、方向均不变,F的方向不变大小可变,f的大小、方向均可变,
但有f≤fmax
而最大静摩擦力fmax=μN=
| ||
| 6 |
右图中,余弦定理得:
| f | 2 max |
| G | 2 x |
解得:FMIN=28.8N;
FMAX=57.7N,
因此28.8N≤F≤57.7N
点评:解法二:先用正交分解法求出GX和F的合力F合,而F合≤fm,
整理后得一元二次不等式,解此不等式同样可得结果.
整理后得一元二次不等式,解此不等式同样可得结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,物块A重10N,物块B重20N,A、B间的动摩擦因数为0.1,B与地面间的动摩擦因数为0.2.现用水平拉力F向左拉物块B,要使A、B发生相对滑动,则F至少为( )
如图所示,物块A重10N,物块B重20N,A、B间的动摩擦因数为0.1,B与地面间的动摩擦因数为0.2.现用水平拉力F向左拉物块B,要使A、B发生相对滑动,则F至少为( )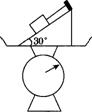
 如图所示,物块A重10N,物块B重20N,A、B间的动摩擦因数为0.1,B与地面间的动摩擦因数为0.2.现用水平拉力F向左拉物块B,要使A、B发生相对滑动,则F至少为
如图所示,物块A重10N,物块B重20N,A、B间的动摩擦因数为0.1,B与地面间的动摩擦因数为0.2.现用水平拉力F向左拉物块B,要使A、B发生相对滑动,则F至少为