题目内容
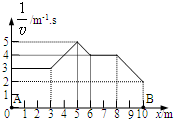 宇航员在太空中沿直线从A点运动到B点,他的运动图象如图所示,图中v是宇航员的速度,x是他的坐标.求:
宇航员在太空中沿直线从A点运动到B点,他的运动图象如图所示,图中v是宇航员的速度,x是他的坐标.求:(1)宇航员从A点运动到B点所需时间.
(2)若宇航员以及推进器等装备的总质量恒为240kg,从A点到B点的过程中宇航员身上背着的推进器做功所消耗的能量为多少?
分析:(1)本题是
-x图象,根据时间)△t=
=△x
,图象与坐标轴所围的“面积”表示时间,根据几何知识求出面积,即可得到宇航员从A点运动到B点所需时间.
(2)根据动能定理求解各段过程推进器做功,即可得到总功.总功等于推进器做功所消耗的总能量.
| 1 |
| v |
| △x |
| v |
| 1 |
| v |
(2)根据动能定理求解各段过程推进器做功,即可得到总功.总功等于推进器做功所消耗的总能量.
解答:解:(1)△t=
,即图线所围的面积△S表示宇航员从A点运动到B点所需时间:
t=S=[3×3+
(3+5)×2+
(5+4)×1+4×2+
(4+2)×2]=35.5s
(2)由动能定理得:
WF=
m
-
m
+
m
-
m
+
m
-
m
=
m(
+
-2
)=
×240×(0.332+0.52-2×0.22)=33.5J
各段过程推进器做功,即是总功,总功等于推进器做功所消耗的总能量,所以进器做功所消耗的能量为33.5J.
答:
(1)宇航员从A点运动到B点所需时间为35.5s.
(2)从A点到B点的过程中宇航员身上背着的推进器做功所消耗的能量为33.5J.
| △x |
| v |
t=S=[3×3+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由动能定理得:
WF=
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 5 |
| 1 |
| 2 |
| v | 2 6 |
| 1 |
| 2 |
| v | 2 5 |
| 1 |
| 2 |
| v | 2 10 |
| 1 |
| 2 |
| v | 2 8 |
| 1 |
| 2 |
| v | 2 3 |
| v | 2 10 |
| v | 2 5 |
| 1 |
| 2 |
各段过程推进器做功,即是总功,总功等于推进器做功所消耗的总能量,所以进器做功所消耗的能量为33.5J.
答:
(1)宇航员从A点运动到B点所需时间为35.5s.
(2)从A点到B点的过程中宇航员身上背着的推进器做功所消耗的能量为33.5J.
点评:本题关键要理解图象面积的物理意义,知道面积表示时间,并能根据动能定理求解做功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
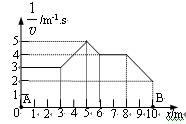
 在太空中沿直线从A点运动到B点,他的运动图像如图所示,图中v是宇航员的速度,x是他的坐标。求:
在太空中沿直线从A点运动到B点,他的运动图像如图所示,图中v是宇航员的速度,x是他的坐标。求:
