题目内容
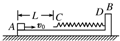
如图所示,LMN是竖直平面内固定的光滑绝缘轨道,MN水平且足够长,LM下端与MN相切.在虚线OP的左侧,有一竖直向下的匀强电场E1,在虚线OP的右侧,有一水平向右的匀强电场E2和垂直纸面向里的匀强磁场B.C、D是质量均为m的小物块(可视为质点),其中C所带的电荷量为+q,D不带电.现将物块D静止放置在水平轨道的MO段,将物块C从LM上某一位置由静止释放,物块C沿轨道下滑进入水平轨道,速度为v,然后与D相碰,粘合在一起继续向右运动.求:

(1)物块C从LM上释放时距水平轨道的高度h;
(2)物块C与D碰后瞬间的共同速度v共;
(3)物块C与D离开水平轨道时与OP的距离x.

(1)物块C从LM上释放时距水平轨道的高度h;
(2)物块C与D碰后瞬间的共同速度v共;
(3)物块C与D离开水平轨道时与OP的距离x.
(1)物块C下滑过程中,由动能定理得:
(mg+qE1)h=
mv2-0,
解得:h=
;
(2)物块C、D碰撞过程动量守恒,以C、D组成的系统为研究对象,以C的初速度方向为正方向,
由动量守恒定律得:mv=(m+m)v共,解得:v共=
;
(3)C与D刚要离开水平轨道时对轨道的压力为零,
设此时它们的速度为v′,在竖直方向上,qv'B=2mg…①
CD一起向右运动过程中,由动能定理得:qE2x=
×2mv′2-
×2m
…②
由①②解得:x=
(
-
);
答:(1)物块C从LM上释放时距水平轨道的高度h=
;
(2)物块C与D碰后瞬间的共同速度v共=
;
(3)物块C与D离开水平轨道时与OP的距离x=
(
-
).
(mg+qE1)h=
| 1 |
| 2 |
解得:h=
| mv2 |
| 2(mg+qE1) |
(2)物块C、D碰撞过程动量守恒,以C、D组成的系统为研究对象,以C的初速度方向为正方向,
由动量守恒定律得:mv=(m+m)v共,解得:v共=
| v |
| 2 |
(3)C与D刚要离开水平轨道时对轨道的压力为零,
设此时它们的速度为v′,在竖直方向上,qv'B=2mg…①
CD一起向右运动过程中,由动能定理得:qE2x=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2共 |
由①②解得:x=
| m2 |
| qE2 |
| 4mg2 |
| q2B2 |
| v2 |
| 4 |
答:(1)物块C从LM上释放时距水平轨道的高度h=
| mv2 |
| 2(mg+qE1) |
(2)物块C与D碰后瞬间的共同速度v共=
| v |
| 2 |
(3)物块C与D离开水平轨道时与OP的距离x=
| m2 |
| qE2 |
| 4mg2 |
| q2B2 |
| v2 |
| 4 |

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目

 平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的
平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的

