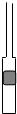题目内容
如图所示，一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭，横截面积S2=4S1．上端与大气连通，管中有一段水银封闭了一定质量的理想气体，空气柱长度为h，水银柱高度h1=h2=h．已知大气压强为po，水银密度为ρ，重力加速度为g，初始温度为To．求：（1）将温度降低至水银柱恰好全部进入粗管中，此时封闭气体的温度；
（2）接着在细管口加一个抽气机，对细管内空气进行抽气（保持第一小问中的温度不变），使水银柱上升至原图示位置，细管内被抽气体的压强．
【答案】分析：（1）根据体积不变，求出水银柱恰好全部进入粗管中时，水银柱的高度，根据理想气体状态方程求解时封闭气体的温度；
（2）抽气过程，封闭气体发生等温变化，根据玻意耳定律求出图示位置的压强，根据压强关系，求解细管内被抽气体的压强．
解答：解：（1）粗管内水银柱长度增加了h2’，根据：S1?h1=S2h2′
得，h2′=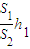
=
封闭气体压强：
根据理想气体状态方程：
=
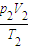
而p1=p+2ρgh，V1=S2h，V2=S2（h-h2′），T1=T，
代入解得：封闭气体的温度：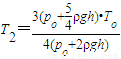
；
（2）抽气过程，封闭气体发生等温变化：
p2V2=p3V3
得
=
=
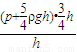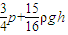
细管内被抽气体的压强：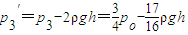
．
答：（1）将温度降低至水银柱恰好全部进入粗管中，此时封闭气体的温度是
；
（2）细管内被抽气体的压强是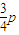
-
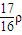gh．
点评：本题一方面要确定气体发生了何种变化，选择物理规律；二要抓住封闭气体与细管内被抽气体的压强进行求解．
（2）抽气过程，封闭气体发生等温变化，根据玻意耳定律求出图示位置的压强，根据压强关系，求解细管内被抽气体的压强．
解答：解：（1）粗管内水银柱长度增加了h2’，根据：S1?h1=S2h2′
得，h2′=
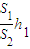=封闭气体压强：
根据理想气体状态方程：
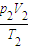
=而p1=p+2ρgh，V1=S2h，V2=S2（h-h2′），T1=T，
代入解得：封闭气体的温度：
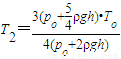； （2）抽气过程，封闭气体发生等温变化：
p2V2=p3V3
得
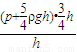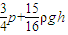
==细管内被抽气体的压强：
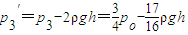． 答：（1）将温度降低至水银柱恰好全部进入粗管中，此时封闭气体的温度是
；（2）细管内被抽气体的压强是
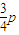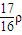-gh．点评：本题一方面要确定气体发生了何种变化，选择物理规律；二要抓住封闭气体与细管内被抽气体的压强进行求解．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
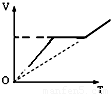
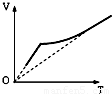
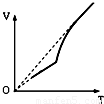
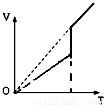
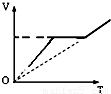
（2011?闵行区二模）如图所示，一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭，上端足够长，下端（粗端）中间有一段水银封闭了一定质量的理想气体．现对气体缓慢加热，气体温度不断升高，水银柱上升，则被封闭气体体积和热力学温度的关系最接近哪个图象（ ）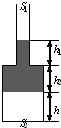
如图所示，一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭，横截面积S2=4S1．上端与大气连通，管中有一段水银封闭了一定质量的理想气体，空气柱长度为h，水银柱高度h1=h2=h．已知大气压强为po，水银密度为ρ，重力加速度为g，初始温度为To．求：
