题目内容
 如图所示,一辆质量是m=2kg的平板车左端放有质量M=3kg的小滑块,滑块与平板车之间的动摩擦因数μ=0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:
如图所示,一辆质量是m=2kg的平板车左端放有质量M=3kg的小滑块,滑块与平板车之间的动摩擦因数μ=0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:(1)平板车每一次与墙壁碰撞后向左运动的最大距离.
(2)平板车第二次与墙壁碰撞前瞬间的速度v.
(3)为使滑块始终不会滑到平板车右端,平板车至少多长?
分析:1、系统总动量向右,平板车速度为零时,滑块还在向右滑行,由动能定理列出等式求解
2、假如平板车在第二次碰撞前还未和滑块相对静止,就违反动量守恒,所以平板车在第二次碰撞前肯定已和滑块具有共同速度.根据动量守恒定律列出等式求解
3、根据能量守恒列出等式求解
2、假如平板车在第二次碰撞前还未和滑块相对静止,就违反动量守恒,所以平板车在第二次碰撞前肯定已和滑块具有共同速度.根据动量守恒定律列出等式求解
3、根据能量守恒列出等式求解
解答:解:(1)设第一次碰墙壁后,平板车向左移动s,速度为0.
由于系统总动量向右,平板车速度为零时,滑块还在向右滑行.
由动能定理得
-μMgS=0-
m
①
s=
②
代入数据得s=
m ③
(2)假如平板车在第二次碰撞前还未和滑块相对静止,那么其速度的大小肯定还是2m/s,滑块的速度则大于2m/s,方向均向右.这样就违反动量守恒.
所以平板车在第二次碰撞前肯定已和滑块具有共同速度v.此即平板车碰墙前瞬间的速度.
Mv0-mv0=(m+M)v ④
∴v=
v0 ⑤
代入数据得v=
v0=0.4m/s ⑥
(3)平板车与墙壁发生多次碰撞,最后停在墙边.设滑块相对平板车总位移为l,
根据能量守恒则有:
(M+m)
=μMgl ⑦
l=
⑧
代入数据得l=
m
l即为平板车的最短长度.
答:(1)平板车每一次与墙壁碰撞后向左运动的最大距离是
m.
(2)平板车第二次与墙壁碰撞前瞬间的速度是0.4m/s.
(3)为使滑块始终不会滑到平板车右端,平板车至少
m
由于系统总动量向右,平板车速度为零时,滑块还在向右滑行.
由动能定理得
-μMgS=0-
| 1 |
| 2 |
| v | 2 0 |
s=
| ||
| 2μMg |
代入数据得s=
| 1 |
| 3 |
(2)假如平板车在第二次碰撞前还未和滑块相对静止,那么其速度的大小肯定还是2m/s,滑块的速度则大于2m/s,方向均向右.这样就违反动量守恒.
所以平板车在第二次碰撞前肯定已和滑块具有共同速度v.此即平板车碰墙前瞬间的速度.
Mv0-mv0=(m+M)v ④
∴v=
| M-m |
| M+m |
代入数据得v=
| 1 |
| 5 |
(3)平板车与墙壁发生多次碰撞,最后停在墙边.设滑块相对平板车总位移为l,
根据能量守恒则有:
| 1 |
| 2 |
| v | 2 0 |
l=
| ||
| 2μMg |
代入数据得l=
| 5 |
| 6 |
l即为平板车的最短长度.
答:(1)平板车每一次与墙壁碰撞后向左运动的最大距离是
| 1 |
| 3 |
(2)平板车第二次与墙壁碰撞前瞬间的速度是0.4m/s.
(3)为使滑块始终不会滑到平板车右端,平板车至少
| 5 |
| 6 |
点评:本题是动量守恒定律和动能定理的综合应用,涉及力在空间的效果,优先考虑能量守恒定律或动能定理.

练习册系列答案
相关题目
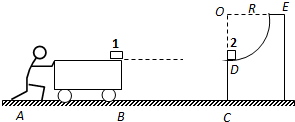 如图所示,一辆质量为M的小车静止在水平面上,车面上右端点有一可视为质点的滑块1,水平面上有与车右端相距为4R的固定的
如图所示,一辆质量为M的小车静止在水平面上,车面上右端点有一可视为质点的滑块1,水平面上有与车右端相距为4R的固定的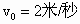 的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取
的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取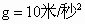 )求:
)求:
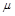 =0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:
=0.4,开始时平板车和滑块共同以v0=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求: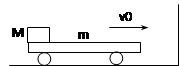
 如图所示,一辆质量是m=2kg的平板车左端放有质量M=3kg的小滑块,滑块与平板车之间的动摩擦因数μ=0.4,开始时平板车和滑块共同以v=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求:
如图所示,一辆质量是m=2kg的平板车左端放有质量M=3kg的小滑块,滑块与平板车之间的动摩擦因数μ=0.4,开始时平板车和滑块共同以v=2m/s的速度在光滑水平面上向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,以至滑块不会滑到平板车右端.(取g=10m/s2)求: