题目内容
6.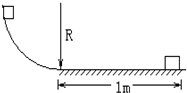 如图,一质量为m=10kg的物体,由$\frac{1}{4}$圆弧轨道上端从静止开始下滑,到达底端时的速度v=2m/s,然后沿水平面向右滑动1m距离后停止.已知轨道半径R=0.4m,g=10m/s2则:
如图,一质量为m=10kg的物体,由$\frac{1}{4}$圆弧轨道上端从静止开始下滑,到达底端时的速度v=2m/s,然后沿水平面向右滑动1m距离后停止.已知轨道半径R=0.4m,g=10m/s2则:(1)物体沿轨道下滑过程中克服摩擦力做多少功?
(2)物体滑至圆弧底端时对轨道的压力是多大?
(3)物体与水平面间的动摩擦因数μ是多少?
分析 (1)物体做圆周运动,由牛顿第二定律可以求出物体受到的支持力,然后由牛顿第二定律求出物体对轨道的压力.
(2)由动能定理可以求出物体下滑过程中克服摩擦力做的功.
(3)物体在水平方向上运动,由动能定理可以求出物体与水平面间的动摩擦因数.
解答 解:(1)物体下滑时,由动能定理得:
mgR-Wf=$\frac{1}{2}$mv2-0,解得:Wf=20J;
(2)在圆弧低端,由牛顿第二定律得:
F-mg=m$\frac{{V}^{2}}{R}$,解得:F=200N,
由牛顿第三定律可知,物体对轨道低端的压力:F′=F=200N;
(3)物体在水平面上做减速运动,
由动能定理得:-μmgx=0-$\frac{1}{2}$mv2,
解得μ=0.2;
答:(1)物体沿轨道下滑过程中克服摩擦力做20J的功.
(2)物体滑至圆弧底端时对轨道的压力是200N.
(3)物体与水平面间的动摩擦因数μ是0.2.
点评 分析清楚物体的运动过程及受力情况,由牛顿定律、动能定理即可正确解题,本题难度不大,是一道基础题.

练习册系列答案
相关题目
17.一个小水电站,输出的电功率为20kW,输电线总电阻为0.5Ω,如果先用400V的电压输送,后又改用2 000V的电压输送,则输送电压提高后,输电导线上损失的电功率变化情况是( )
| A. | 减少50 W | B. | 减少1 200 W | C. | 减少7.68×106 W | D. | 增大7.68×106 W |
14. 如图所示为交流发电机的结构示意图,在匀强磁场中有一矩形线圈abcd与交流电流表A、小灯泡串联.使矩形线圈以恒定角速度绕过bc、ad中点的轴线旋转.下列表述正确的是( )
如图所示为交流发电机的结构示意图,在匀强磁场中有一矩形线圈abcd与交流电流表A、小灯泡串联.使矩形线圈以恒定角速度绕过bc、ad中点的轴线旋转.下列表述正确的是( )
 如图所示为交流发电机的结构示意图,在匀强磁场中有一矩形线圈abcd与交流电流表A、小灯泡串联.使矩形线圈以恒定角速度绕过bc、ad中点的轴线旋转.下列表述正确的是( )
如图所示为交流发电机的结构示意图,在匀强磁场中有一矩形线圈abcd与交流电流表A、小灯泡串联.使矩形线圈以恒定角速度绕过bc、ad中点的轴线旋转.下列表述正确的是( )| A. | 交流电流表A的示数随时间按余弦规律变化 | |
| B. | 线圈转动的角速度越大,交流电流表A的示数越大 | |
| C. | 线圈平面与磁场平行时,流经小灯泡的电流最大 | |
| D. | 线圈平面与磁场垂直时,流经小灯泡的电流最大 |
15.关于运动的合成与分解,下述说法中正确的是( )
| A. | 合运动的速度大小等于分运动的速度大小之和 | |
| B. | 两个直线运动的合运动一定是直线运动 | |
| C. | 两个曲线运动的合运动一定是曲线运动 | |
| D. | 合运动和分运动具有同时性 |
16. 如图所示,带电质点P静止于两平行金属板间,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )
如图所示,带电质点P静止于两平行金属板间,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )
 如图所示,带电质点P静止于两平行金属板间,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )
如图所示,带电质点P静止于两平行金属板间,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )| A. | 电压表读数增大 | B. | 电流表读数减小 | ||
| C. | 质点将向上运动 | D. | R2消耗的功率增大 |

 滑雪运动员以一定的速度从水平台的O点水平飞出,落地点A到飞出点O得距离OA=27m,山坡与水平面的夹角α=37°.不计空气阻力.(已知sin37°=0.6,cos37°=0.8,g取10m/s2)求:
滑雪运动员以一定的速度从水平台的O点水平飞出,落地点A到飞出点O得距离OA=27m,山坡与水平面的夹角α=37°.不计空气阻力.(已知sin37°=0.6,cos37°=0.8,g取10m/s2)求: 一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,并且波刚好传到x=4m处,再经0.3s时间质点a第一次达到波峰位置,则质点b刚开始振动时的运动方向为沿y轴向上,质点b第一次出现在波峰的时刻为0.5s.
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,并且波刚好传到x=4m处,再经0.3s时间质点a第一次达到波峰位置,则质点b刚开始振动时的运动方向为沿y轴向上,质点b第一次出现在波峰的时刻为0.5s.