题目内容
(18分)一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后木板运动的速度一时间图像如图所示。已知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上。取重力加速度的大小g="10" m/s2,求: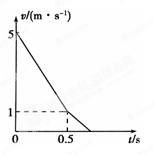
(1)物块与木板间的动摩擦因数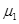 ;
;
(2)木板与地面间的动摩擦因数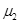 ;
;
(3)从0.5s到停止,物块与木板的加速度分别多大;
(4)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小。
解析试题分析:(1)设物块和木板间的质量为m,物块和木板间,木板与地面间的动摩擦因数分别为 ,
,
从t=0时刻,木板与物块之间的摩擦力使物块加速,此过程一直持续到物块和木板具有共同速度为止,由图可知,在 时,物块和木板的速度相同,设t=0到
时,物块和木板的速度相同,设t=0到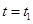 时间间隔内,物块加速度为
时间间隔内,物块加速度为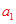 ,则
,则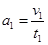 (1分)
(1分)
由牛顿第二定律得: (1分)
(1分)
解得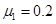 (1分)
(1分)
(2) (1分)
(1分) (2分)
(2分)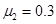 (1分)
(1分)
或中 、
、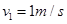 分别为木板在t=0到
分别为木板在t=0到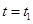 时的速度大小
时的速度大小
(3)在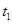 时刻后,地面对木板的摩擦力阻碍木板运动,物块与木板之间的摩擦力改变方向。设物块与木板之间的摩擦力大小为
时刻后,地面对木板的摩擦力阻碍木板运动,物块与木板之间的摩擦力改变方向。设物块与木板之间的摩擦力大小为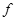 ,物块和木板的加速度大小分别为
,物块和木板的加速度大小分别为 和
和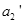 ,则由牛顿第二定律得
,则由牛顿第二定律得 (1分)
(1分) (1分)
(1分)
假设二者相对静止,则 ;得
;得 ,与假设矛盾,则二者相对滑动,故
,与假设矛盾,则二者相对滑动,故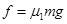 (1分)
(1分)
代入解出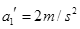 (1分)
(1分)  (1分)
(1分)
(4)可知木块减速到零后就静止,物块一直减速到静止,物块的 图像如图中点划线所示。由运动学公式可推知,物块和木板相对于地面的运动距离分别为
图像如图中点划线所示。由运动学公式可推知,物块和木板相对于地面的运动距离分别为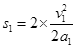 (2分)
(2分)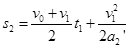 (2分)
(2分)
物块相对于木板的位移的大小为 (1分)
(1分)
联得 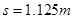 (1分)
(1分)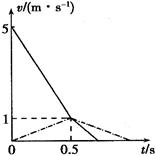
考点:牛顿运动定律的综合应用,V—t图象,

 科学实验活动册系列答案
科学实验活动册系列答案某一质点运动的位移 x 随时间 t 变化的图象如图所示,则( )
| A.第10s末,质点的速度最大 |
| B.0~10s内,质点所受合外力的方向与速度方向相反 |
| C.第5s末和第15s末,质点的加速度方向相反 |
| D.在20s内,质点的位移为9m |
将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的过程中,v—t图像如图所示。以下判断正确的是
| A.前3s内货物处于超重状态 |
| B.最后2s内货物只受重力作用 |
| C.前3s内与最后2s内货物的平均速度相同 |
| D.第3s末至第5S末的过程中,货物的机械能守恒 |
如图所示容器内盛有水,器壁AB呈倾斜状,有一个小物块P处于图示状态,并保持静止,则该物体受力情况正确的是( )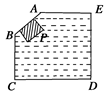
| A.P可能只受一个力 |
| B.P可能只受三个力 |
| C.P不可能只受二个力 |
| D.P不是受到二个力就是四个力 |
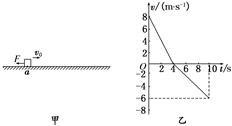
 —t图像如图乙,试求:(g=10m/s2)
—t图像如图乙,试求:(g=10m/s2)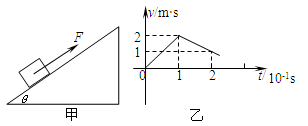

 沿斜面向上推出(斜面足够长且与水平方向的倾角
沿斜面向上推出(斜面足够长且与水平方向的倾角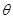 可调节),设物体在斜面上能达到的最大位移为
可调节),设物体在斜面上能达到的最大位移为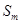 ,实验测得
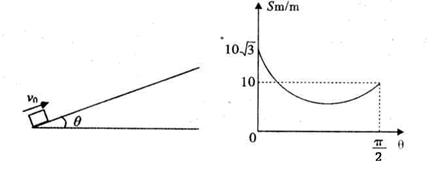
,实验测得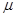 。
。

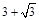 )s相遇
)s相遇 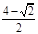 s相遇
s相遇