题目内容
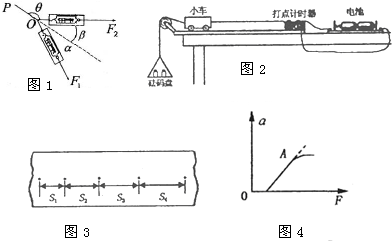
(1)如图1,固定于竖直面内的粗糙斜杆,在水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力作用下,小球沿杆由底端匀速运动到顶端,为使拉力做功最小,拉力F与杆的夹角α=

(2)如图2所示,物体A、B、C放在光滑水平面上用细线a b连接,力F作用在A上,使三物体在水平面上运动,若在B上放一小物体D,D随B一起运动,且原来的拉力F保持不变,那么加上物体D后两绳中拉力的变化是Ta
(3)如图3所示,在场强大小为E的匀强电场中,一根长为L的不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零,则电场强度E=
;运动过程中的最大动能EKm=
60°
60°
,拉力大小F=mg
mg
.
(2)如图2所示,物体A、B、C放在光滑水平面上用细线a b连接,力F作用在A上,使三物体在水平面上运动,若在B上放一小物体D,D随B一起运动,且原来的拉力F保持不变,那么加上物体D后两绳中拉力的变化是Ta
变大
变大
,Tb变小
变小
.(回答变大、变小或不变)(3)如图3所示,在场强大小为E的匀强电场中,一根长为L的不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零,则电场强度E=
| ||
| q |
| ||
| q |
(2-
)mgL
| 3 |
(2-
)mgL
.| 3 |
分析:(1)拉力要做功最小,就是要摩擦力等于零,将力F按沿杆和垂直于杆进行受力分解,求解拉力的最小值.
(2)根据牛顿第二定律,对整体进行研究加速度,再分别以A和C为研究对象,研究两绳拉力的变化.
(3)小球从A到B过程中重力和电场力做功,动能的变化量为零,根据动能定理求解电场强度.当重力与电场力的合力沿绳子方向时,动能最大.由两力的关系求出此时绳子与水平方向的夹角,再由动能定理求解最大动能.
(2)根据牛顿第二定律,对整体进行研究加速度,再分别以A和C为研究对象,研究两绳拉力的变化.
(3)小球从A到B过程中重力和电场力做功,动能的变化量为零,根据动能定理求解电场强度.当重力与电场力的合力沿绳子方向时,动能最大.由两力的关系求出此时绳子与水平方向的夹角,再由动能定理求解最大动能.
解答:解:
(1)当摩擦力做功为零时,拉力做功最小.将力F按沿杆和垂直于杆进行受力分解,得
mgsin30°=Fcosα①
mgcos30°=Fsinα②
由①②联立解得:F=mg,α=60°
(2)加上物体D后,根据牛顿第二定律分析可知,整体的加速度a减小.
以C为研究对象得 Tb=mba,a减小,mb不变,Tb变小
以A为研究对象得 F-Ta=maa,a减小,F,ma不变,Ta变大.
(3)根据动能定理得
A到B过程:mgLsinθ-qEL(1-cosθ)=0
代入解得 E=
当重力与电场力的合力沿绳子方向时,动能最大.设此时绳子与水平方向的夹角为α,则
tanα=
=
,α=30°
再由动能定理得
mgLsinα-qEL(1-cosα)=Ekm
解得,运动过程中小球的最大动能EKm=(2-
)mgL
故答案为:
(1)60°,mg
(2)变大,变小
(3)
,(2-
)mgL
(1)当摩擦力做功为零时,拉力做功最小.将力F按沿杆和垂直于杆进行受力分解,得
mgsin30°=Fcosα①
mgcos30°=Fsinα②
由①②联立解得:F=mg,α=60°
(2)加上物体D后,根据牛顿第二定律分析可知,整体的加速度a减小.
以C为研究对象得 Tb=mba,a减小,mb不变,Tb变小
以A为研究对象得 F-Ta=maa,a减小,F,ma不变,Ta变大.
(3)根据动能定理得
A到B过程:mgLsinθ-qEL(1-cosθ)=0
代入解得 E=
| ||
| q |
当重力与电场力的合力沿绳子方向时,动能最大.设此时绳子与水平方向的夹角为α,则
tanα=
| mg |
| qE |
| ||
| 3 |
再由动能定理得
mgLsinα-qEL(1-cosα)=Ekm
解得,运动过程中小球的最大动能EKm=(2-
| 3 |
故答案为:
(1)60°,mg
(2)变大,变小
(3)
| ||
| q |
| 3 |
点评:本题整合了力的分解、牛顿第二定律、动能定理等规律,综合性较强,但分析受力情况和运动情况是关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 (1)如图所示,甲图中游标卡尺的读数为______cm.
(1)如图所示,甲图中游标卡尺的读数为______cm.
(2)如图乙所示,在探究“共点力合成”的实验中,橡皮条一端固定于P点,另一端连接两个弹簧秤,分别用F1与F2拉两个弹簧秤,将结点拉至O点.现让F2大小增大,方向不变,要使结点仍位于O点,则F1的大小及图中β(β>90°)角的变化可能是______
A、增大F1的同时增大β角 B、减小F1的同时减小β角
C、增大F1的同时减小β角 D、减小F1的同时增大β角
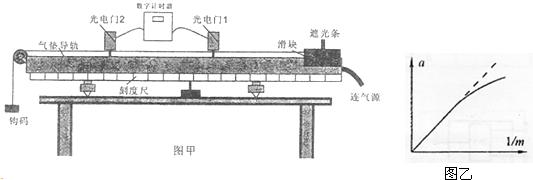
(3)某实验小组利用如图甲所示的实验装置来探究当合外力一定时,物体运动的加速度与其质量之间的关系.
①由图甲中刻度尺读出两个光电门中心之间的距离S,由游标卡尺测得遮光条的宽度d,由数字计时器可以读出遮光条通过电门1的时间△t1和遮光条通过光电门2的时间△t2,滑块的加速度的表达式为______.(以上表达式均用字母表示)
②在本次实验中,实验小组通过改变滑块质量做了6组实验,得到如下表的实验数据,
| m(g) | a(m/s2) |
| 250 | 1.80 |
| 300 | 1.50 |
| 350 | 1.29 |
| 400 | 1.13 |
| 500 | 0.90 |
| 800 | 0.56 |
 的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.
的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.
(1)如图所示,甲图中游标卡尺的读数为______cm.
(2)如图乙所示,在探究“共点力合成”的实验中,橡皮条一端固定于P点,另一端连接两个弹簧秤,分别用F1与F2拉两个弹簧秤,将结点拉至O点.现让F2大小增大,方向不变,要使结点仍位于O点,则F1的大小及图中β(β>90°)角的变化可能是______
A、增大F1的同时增大β角 B、减小F1的同时减小β角
C、增大F1的同时减小β角 D、减小F1的同时增大β角
(3)某实验小组利用如图甲所示的实验装置来探究当合外力一定时,物体运动的加速度与其质量之间的关系.
①由图甲中刻度尺读出两个光电门中心之间的距离S,由游标卡尺测得遮光条的宽度d,由数字计时器可以读出遮光条通过电门1的时间△t1和遮光条通过光电门2的时间△t2,滑块的加速度的表达式为______.(以上表达式均用字母表示)
②在本次实验中,实验小组通过改变滑块质量做了6组实验,得到如下表的实验数据,
根据实验数据作出了a与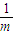 的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.
的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.


(2)如图乙所示,在探究“共点力合成”的实验中,橡皮条一端固定于P点,另一端连接两个弹簧秤,分别用F1与F2拉两个弹簧秤,将结点拉至O点.现让F2大小增大,方向不变,要使结点仍位于O点,则F1的大小及图中β(β>90°)角的变化可能是______
A、增大F1的同时增大β角 B、减小F1的同时减小β角
C、增大F1的同时减小β角 D、减小F1的同时增大β角
(3)某实验小组利用如图甲所示的实验装置来探究当合外力一定时,物体运动的加速度与其质量之间的关系.
①由图甲中刻度尺读出两个光电门中心之间的距离S,由游标卡尺测得遮光条的宽度d,由数字计时器可以读出遮光条通过电门1的时间△t1和遮光条通过光电门2的时间△t2,滑块的加速度的表达式为______.(以上表达式均用字母表示)
②在本次实验中,实验小组通过改变滑块质量做了6组实验,得到如下表的实验数据,
| m(g) | a(m/s2) |
| 250 | 1.80 |
| 300 | 1.50 |
| 350 | 1.29 |
| 400 | 1.13 |
| 500 | 0.90 |
| 800 | 0.56 |
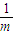 的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.
的图线如图乙所示,该图线有一段是弯曲的,试分析图线弯曲的原因______.

 如图所示,下面部分是由电动势为E内阻不计的电源,定值电阻R0和可变电阻R组成的一个闭合电路.上面部分是真空中固定于A点的电量为Q(Q>0)点电荷,另有一电子枪.求:
如图所示,下面部分是由电动势为E内阻不计的电源,定值电阻R0和可变电阻R组成的一个闭合电路.上面部分是真空中固定于A点的电量为Q(Q>0)点电荷,另有一电子枪.求: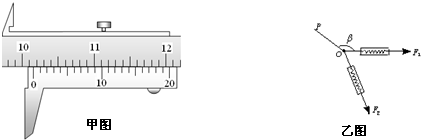 (1)如图所示,甲图中游标卡尺的读数为
(1)如图所示,甲图中游标卡尺的读数为