��Ŀ����
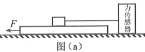
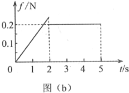
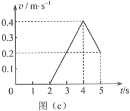
����Ŀ����ͼ����ʾ���ᵯ����ֱ���ã��¶˹̶���ˮƽ�����ϣ�һ����Ϊm��С���뵯���϶˸�h���ɾ�ֹ�ͷš�ijͬѧ̽��С���ڽӴ����ɺ����µ��˶����̣�����С��ʼ�����λ��Ϊԭ�㣬����ֱ���·�����������Ox������С�����ܵ���F��С��С�������λ������x�ı仯��ϵ��ͼ����ʾ�����ƿ����������������ٶ�Ϊg�������ж���ȷ����

A.��x=h+x0ʱ�����������뵯������֮����СB.��͵������Ϊx=h+2x0
C.С���ܵ��ĵ������ֵ����2mgD.С���ܵ����ֵΪ![]()
���𰸡�AD
��������
��ͼ����С����˶�����Ϊ:�����������˶������뵯����Ӵ����������ٶȼ�С�ļ����˶���Ȼ�������ٶ�����ļ����˶���ֱ��С���ٶ�Ϊ�㡣
A����x=h+x0ʱ�������������������ٶ�Ϊ�㣬С���ٶ�������������ϵͳ��е���غ㣬�������������뵯������֮����С��A��ȷ��
B������͵�С���ٶ�Ϊ�㣬�Ӹ��ͷ�С��С���˶�����͵㣬С���ܱ仯��Ϊ�㣬�������Ĺ��͵������Ĺ��ľ���ֵ��ȣ�������͵�ͼ��ʵ����x��Χ�ɵ����Ӧ����mg����������x��Χ�ɵ������ͬ��������͵�Ӧ����h+2x0С��ĺ�ߣ�B����
C����B֪����͵�λ�ô���![]() �����Ե�������2mg�� C����
�����Ե�������2mg�� C����
D����x=h+x0ʱ�������������������ٶ�Ϊ�㣬С���ٶ����������ɶ��ܶ����ɵ�
![]() ��
��
��D��ȷ��