题目内容
某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为va,则过近日点时行星的速率vb为( )
A、vb=
| ||||
B、vb=
| ||||
C、vb=
| ||||
D、vb=
|
分析:根据开普勒第二定律:行星与太阳的连线在相等时间内扫过的面积相等,取极短时间△t,根据“面积”相等列方程得出远日点时与近日点时的速度比值求解.
解答:解:取极短时间△t,
根据开普勒第二定律得行星与太阳的连线在相等时间内扫过的面积相等,
a?va?△t=
b?vb?△t
得到:vb=
vb.
故选:D.
根据开普勒第二定律得行星与太阳的连线在相等时间内扫过的面积相等,
| 1 |
| 2 |
| 1 |
| 2 |
得到:vb=
| a |
| b |
故选:D.
点评:本题考查对开普勒第二定律的理解和应用能力.在极短时间内,行星与太阳连线扫过的范围近似为三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
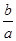 va
B.vb=
va
B.vb=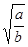 va
C.vb=
va
C.vb=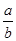 va
D.vb=
va
D.vb=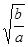 va
va