题目内容
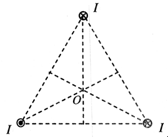
三根相互平行的通电长直导线放在等边三角形的三个顶点上,右图为其截面图,电流方向如图所示。若每根导线的电流均为I,每根直导线单独存在时,在三角形中心O点产生的磁感应强度大小都是B,则三根导线同时存在时O点的磁感应强度大小为( )

| A.0 | B.B | C.2B | D. B B |
C
分析:三角形中心O点到三根导线的距离相等.根据安培定则判断三根导线在O点产生的磁感应强度的方向,根据平行四边形定则进行合成,求出三根导线同时存在时的磁感应强度大小.
解答:解:根据安培定则判断得知:三根导线在O点产生的磁感应强度的方向分别为:上面导线产生的B方向水平向左,大小为B;
下面左边导线产生的B方向斜向左上方,与水平成60°角,
下面右边导线产生的B方向斜向右上方,与水平成60°角,
则根据平行四边形定则进行合成可知,下面两根导线产生的合场强大小为B,方向水平向左,所以三根导线同时存在时的磁感应强度大小为2B,方向水平向左.
故选C
点评:本题首先运用安培定则判断B的方向,其次要利用平行四边形定则进行合成,同时要利用好几何关系.
解答:解:根据安培定则判断得知:三根导线在O点产生的磁感应强度的方向分别为:上面导线产生的B方向水平向左,大小为B;
下面左边导线产生的B方向斜向左上方,与水平成60°角,
下面右边导线产生的B方向斜向右上方,与水平成60°角,
则根据平行四边形定则进行合成可知,下面两根导线产生的合场强大小为B,方向水平向左,所以三根导线同时存在时的磁感应强度大小为2B,方向水平向左.
故选C
点评:本题首先运用安培定则判断B的方向,其次要利用平行四边形定则进行合成,同时要利用好几何关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



