Question

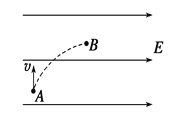
【题目】如图,用跨过光滑定滑轮的缆绳将海面上一搜失去动力的小船沿直线拖向岸边。已知拖动缆绳的电动机功率恒为P=2kW,小船的质量为m=1.0×103kg,小船受到的阻力大小恒为重力的0.1倍，经过A点时的绳子的速度大小为=1.6m/s，绳子与水平面的夹角是37°，小船从A点沿直线加速运动到B点经历时间为t1=2s，A、B两点间距离为d=2m,缆绳质量忽略不计。(sin37°=0.6，cos37°=0.8，g=10 m／s2) 求：

（1）小船在A点的速度；

（2）小船从A点运动到B点的全过程克服阻力做的功Wf；；

（3）若小船经过B点时绳子与水平面的夹角为45°，小船的速度大小4m/s，求小船的加速度大小。

Answer 1

【答案】

【解析】(1)经过A点时的绳子的速度大小为v=1.6m/s，绳子与水平面的夹角是37,那么小船沿绳子收缩方向的速度为v,所以,小船在A点的速度vA= =2m/s；

(2)小船从A点到达B点,受到的阻力恒为f,方向向左,故其克服阻力做的功为：Wf=fd=0.1mgd=2×103J；

(3)若小船经过B点时绳子与水平面的夹角为45,那么,绳子收缩速度v′=vBcos45°=2m/s,所以,绳子的拉力F= =1000N；

对小船应用牛顿第二定律可得：Fcos450.1mg=ma,所以,a= ,故小船的加速度大小为1；