题目内容
如图所示，有一个正方形ABCD，E、F分别为BC和CD的中点，有一个小球从A点由静止开始沿着三个光滑斜面AC、AE、AF分别下滑到C、E、F三点，所用时间依次表示为t1、t2、t3，则（ ）
| A．t1＞t2＞t3 | B．t2＞t1＞t3 |
| C．t3＞t1＞t2 | D．以上判断均不正确 |
设正方形的边长为l，斜面AC、AE、AF与AD的夹角分别为θ1、θ2、θ3，根据几何关系可知：AC=
l、AE=AF=
l，
根据牛顿第二定律得：a1=
=5
m/s，a2=
=4
m/s，a3=
=2
m/s
小球沿斜面AC、AE、AF做匀加速直线运动，根据运动学基本公式得：
x=
at2
解得：t=
所以t1=
=
，t2=
=
，t3=
=
所以t3＞t1＞t2
故选C
| 2 |
| ||
| 2 |
根据牛顿第二定律得：a1=
| mgsinθ1 |
| m |
| 2 |
| mgsinθ2 |
| m |
| 5 |
| mgsinθ3 |
| m |
| 5 |
小球沿斜面AC、AE、AF做匀加速直线运动，根据运动学基本公式得：
x=
| 1 |
| 2 |
解得：t=
|
所以t1=
|
|
|
|
|
|
所以t3＞t1＞t2
故选C
练习册系列答案
世纪百通期末金卷系列答案
相关题目
（2013?开封一模）如图所示，有一个等腰直角三角形的匀强磁场区域，其直角边长为L，磁场方向垂直纸面向外，磁感应强度大小为B．一边长为L总电阻为R的正方形导线框abcd，从图示位置开始沿x轴正方向以速度v匀速穿过磁 场区域．取沿a→b→c→d→a的感应电流为正，则表示线框中电流i随bC边的位置坐标x变化的图象正确的是（ ）
在直角坐标系xOy中，有一半径为R的圆形匀强磁场区域，磁感应强度为B，磁场方向垂直xOy平面指向纸面内，该区域的圆心坐标为（R，0），如图所示，有一个质量为m、带电荷量为-q的离子，由静止经电场加速后从点（0，
如图所示，有一个等腰直角三角形的匀强磁场区域，其直角边长为L，磁场方向垂直纸面向外，磁感应强度大小为B．边长为L、总电阻为R的正方形导线框abcd，从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域．取沿a→b→c→d→a的感应电流为正，则下图中表示线框中电流i随bc边的位置坐标x变化的图象正确的是（ ）
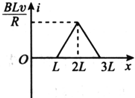
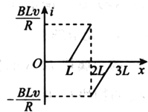
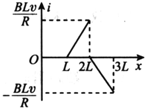
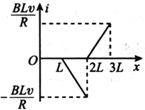
)越高
)越高