题目内容
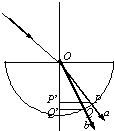
 如图所示,一束细的复色光从空气中射到半球形玻璃体球心O点,经折射分为a、b两束光,分别由P、Q两点射出玻璃体.PP′、QQ′均与过O点的界面法线垂直.设光线a、b在玻璃体内穿行所用时间分别为ta、tb,则ta:tb等于( )
如图所示,一束细的复色光从空气中射到半球形玻璃体球心O点,经折射分为a、b两束光,分别由P、Q两点射出玻璃体.PP′、QQ′均与过O点的界面法线垂直.设光线a、b在玻璃体内穿行所用时间分别为ta、tb,则ta:tb等于( )分析:根据几何知识求出两束光折射角的正弦之比,由折射定律求出折射率之比,由v=
求出光在玻璃体中传播速度之比,再求出ta:tb.
| c |
| n |
解答:解:设半球形玻璃体的半径为R.由图得到,光线a的折射角正弦为:
sinra=sin∠POP′=
=
光线b的折射角正弦为:
sinrb=sin∠QOQ′=
=
两光束的入射角相同,设为i,根据折射定律n=
得玻璃体对两光束的折射率之比为:
na:nb=sinrb:sinra=
:
=QQ′:PP′
由v=
得到,光在玻璃体中传播速度之比为:
va:vb=nb:na
光在玻璃体中传播的距离都为S=R,由公式t=
得:
ta:tb=vb:va=na:nb=QQ′:PP′
故选A
sinra=sin∠POP′=
| P′P |
| OP |
| P′P |
| R |
光线b的折射角正弦为:
sinrb=sin∠QOQ′=
| Q′Q |
| OP |
| Q′Q |
| R |
两光束的入射角相同,设为i,根据折射定律n=
| sini |
| sinr |
na:nb=sinrb:sinra=
| Q′Q |
| R |
| P′P |
| R |
由v=
| c |
| n |
va:vb=nb:na
光在玻璃体中传播的距离都为S=R,由公式t=
| S |
| v |
ta:tb=vb:va=na:nb=QQ′:PP′
故选A
点评:本题考查了光在玻璃体传播速度与折射率的关系,运用几何知识确定折射率的关系是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目