Question

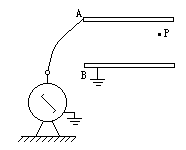
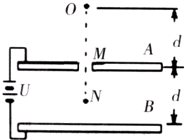如图，A．B为平行板电容器，两板相距d，接在电压为U的电源上，在A板的中央有一小孔M（两板间电场可视为匀强电场）．今有一质量为m的带电质点，自A板上方与A板相距也为d的O点由静止自由下落，穿过小孔M后到达距B板

d

2

的N点时速度恰好为零．（重力加速度为g）求：
（1）带电质点的电荷量，并指出其带电性质；
（2）在保持与电源相连的情况下，A板往下移

d

4

的距离．质点仍从O点由静止自由下落，求质点下落速度为零时距B板的距离．

Answer 1

分析：（1）一带电质点自A板上方相距为h的O点由静止自由下落，先做自由落体运动到M点，到达N时速度恰好为零，说明在MN间做减速运动，合外力向上，所以电场力方向向上，从而判断质点带点情况，根据动能定理求解电荷量；
（2）应用动能定理可以求出质点下落速度为零时距B板的距离．

解答：解：（1）质点先做自由落体运动到M点，到达N处时速度恰好为零，说明在MN间做减速运动，
合外力向上，所以电场力方向向上，而电场强度方向向下，所以质点带负电；
两极板间的场强E：U=Ed  ①，
设电量大小为q，则从O到N点，
由动能定理可得：mg(d+

d

2

)-Eq

d

2

=0 ②，
由①②解得：q=

3mgd

U

  ③；
（2）当A板下移

d

4

时，两板间的距离d′=d-

d

4

=

3d

4

 ④，
两板间的场强E'：U=E′d′⑤，
设下落速度为零时距B板距离为△d，
从开始下落到速度为零的过程中，
由动能定理得：mg(2d-△d)-E′q(

3d

4

-△d)=0  ⑥，
由③④⑤⑥解得：△d=

d

3

；
答：（1）带电质点的电荷量为

3mgd

U

，质点带负电；
（2）质点下落速度为零时距B板的距离为

d

3

．

点评：本题主要考查了动能定理的直接应用，要求同学们会根据受力情况判断质点的带点情况，难度适中．