题目内容
10. 如图,一半径为R的圆表示一柱形区域的横截面(纸面).在柱形区域内加一方向垂直于纸面的匀强磁场,一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域,在圆上的b点离开该区域,离开时速度方向与直线垂直.圆心O到直线的距离为.现将磁场换为平等于纸面且垂直于直线的匀强电场,同一粒子以同样速度沿直线在a点射入柱形区域,也在b点离开该区域.若磁感应强度大小为B,不计重力,求电场强度的大小.
如图,一半径为R的圆表示一柱形区域的横截面(纸面).在柱形区域内加一方向垂直于纸面的匀强磁场,一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域,在圆上的b点离开该区域,离开时速度方向与直线垂直.圆心O到直线的距离为.现将磁场换为平等于纸面且垂直于直线的匀强电场,同一粒子以同样速度沿直线在a点射入柱形区域,也在b点离开该区域.若磁感应强度大小为B,不计重力,求电场强度的大小.
分析 通过带电粒子在磁场中做圆周运动,根据几何关系求出轨道半径的大小.带电粒子在匀强电场中做类平抛运动,结合在沿电场方向上做匀加速直线运动和垂直于电场方向做匀速直线运动,求出电场强度与磁感应强度的大小关系.
解答 解:粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$…①
过b点和O点作直线的垂线,分别与直线交于c和d点.由几何关系知,
线段:ca、bc和过a、b两点的轨迹圆弧的两条半径(未画出)围成一正方形.
因此:ac=bc=r…②
设cd=x,由几何关系得:ac=$\frac{4}{5}$R+x…③bc=$\frac{3}{5}$R+$\sqrt{{R}^{2}-{x}^{2}}$…④
联立②③④式得 r=$\frac{7}{5}$R ⑤
再考虑粒子在电场中的运动.设电场强度的大小为E,粒子在电场中做类平抛运动.
设其加速度大小为a,由牛顿第二定律得:qE=ma…⑥
粒子在电场方向和直线方向所走的距离均为r,
由运动学公式得r=$\frac{1}{2}$at2…⑦r=vt…⑧
式中t是粒子在电场中运动的时间.联立①⑤⑥⑦⑧式得E=$\frac{14qR{B}^{2}}{5m}$;
答:电场强度的大小为$\frac{14qR{B}^{2}}{5m}$.
点评 解决本题的关键掌握带电粒子在磁场中磁偏转和在电场中电偏转的区别,知道磁偏转做匀速圆周运动,电偏转做类平抛运动.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
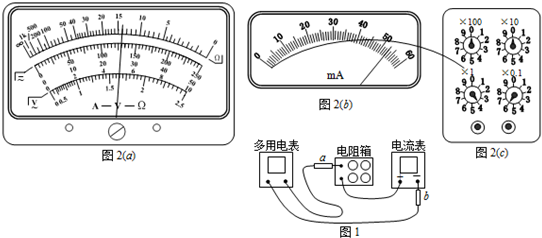
11. 电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电流表A:量程0〜600mA,内阻约2Ω
电流表G:量程0〜500 ?A,内阻Rg=200Ω
电压表V:量程0〜3V,内阻约5kΩ
定值电阻R1=19800Ω
定值电阻R2=9800Ω
滑动变阻器R3:0〜100Ω,1A
滑动变阻器R4:0〜1000Ω,1A
电键一只,导线若干
待测电瓶E
(1)请选择合适的器材在下边虚线框中画出实验电路图(器材必须标明符号).
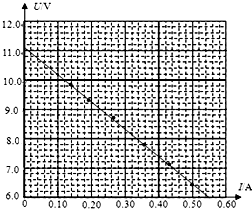
(2)兴趣小组记录了实验数据,并通过计算得到了6组电压U和对应电流I的值,作出了U-I图象.由图象可得这块旧电瓶的电动势为11.1V,内阻为9.5Ω
 电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:电流表A:量程0〜600mA,内阻约2Ω
电流表G:量程0〜500 ?A,内阻Rg=200Ω
电压表V:量程0〜3V,内阻约5kΩ
定值电阻R1=19800Ω
定值电阻R2=9800Ω
滑动变阻器R3:0〜100Ω,1A
滑动变阻器R4:0〜1000Ω,1A
电键一只,导线若干
待测电瓶E
(1)请选择合适的器材在下边虚线框中画出实验电路图(器材必须标明符号).
(2)兴趣小组记录了实验数据,并通过计算得到了6组电压U和对应电流I的值,作出了U-I图象.由图象可得这块旧电瓶的电动势为11.1V,内阻为9.5Ω
| 电压U/V | 9.80 | 9.30 | 8.70 | 7.80 | 7.13 | 6.42 |
| 电流I/A | 0.14 | 0.19 | 0.26 | 0.35 | 0.43 | 0.50 |
1. 喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
 喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )| A. | 向正极板偏转 | B. | 电场力对墨滴做负功 | ||
| C. | 运动轨迹是抛物线 | D. | 电势能逐渐增大 |
2.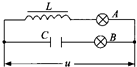 如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将它们接在电压为u的交流电源上,两只灯泡的亮度一样.若保持电源电压的有效值不变,( )
如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将它们接在电压为u的交流电源上,两只灯泡的亮度一样.若保持电源电压的有效值不变,( )
 如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将它们接在电压为u的交流电源上,两只灯泡的亮度一样.若保持电源电压的有效值不变,( )
如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将它们接在电压为u的交流电源上,两只灯泡的亮度一样.若保持电源电压的有效值不变,( )| A. | 将电源频率增大,A灯泡变暗,B灯泡变亮 | |
| B. | 将电源频率增大,A灯泡变亮,B灯泡变暗 | |
| C. | 将交流电源换成直流,A灯泡变暗,B灯泡变亮 | |
| D. | 将交流电源换成直流,A灯泡变亮,B灯泡变暗 |
19.张明同学双手握住竖直竹竿匀速攀上和匀速滑下的过程中,张明受到的摩擦力分别为f1和f2,那么( )
| A. | f1方向竖直向下,f2方向竖直向上,且f1=f2 | |
| B. | fl方向竖直向上,f2方向竖直向上,且f1=f2 | |
| C. | f1为静摩擦力,f2为滑动摩擦力,且f1>f2 | |
| D. | f1为静摩擦力,f2为静摩擦力 |
20.关于速度和加速度的关系,下列说法中正确的是( )
| A. | 加速度的正、负表示了物体运动的方向 | |
| B. | 加速度越来越大,则速度越来越大 | |
| C. | 运动的物体加速度减小,表示物体做减速运动 | |
| D. | 加速度的方向与初速度方向相同时,物体的运动速度将增大 |
 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.