题目内容
6.A、B两行星在同一平面内绕同一恒星做匀速圆周运动,运行方向相同,A的轨道半径为r1,B的轨道半径为r2,已知恒星质量为m,恒星对行星的引力远大于行星间的引力,两行星的轨道半径r1<r2.若在某一时刻两行星相距最近,试求:再经过多少时间两行星距离又最近?分析 A、B两行星距离最近时A、B与恒星在同一条圆半径上.根据恒星对行星的万有引力提供向心力列式,得到行星角速度的表达式.根据A、B距离最近的条件是:ω1t-ω2t=n×2π(n=1,2,3…),求出时间.
解答 解:A、B两行星距离最近时A、B与恒星在同一条圆半径上. A、B运动方向相同,A更靠近恒星,A的转动角速度大、周期短.如果经过时间t,A、B与恒星连线半径转过的角度相差2π的整数倍,则A、B与恒星又位于同一条圆半径上,距离最近.
设A、B的角速度分别为ω1,ω2,经过时间t,A转过的角速度为ω1t,B转过的角度为ω2t.A、B距离最近的条件是:ω1t-ω2t=n×2π(n=1,2,3…)
恒星对行星的引力提供向心力,则:$\frac{GMm}{{r}^{2}}=m{ω}^{2}r$
解得:$ω=\sqrt{\frac{GM}{{r}^{3}}}$
由此得出:${ω}_{1}=\sqrt{\frac{GM}{{{r}_{1}}^{3}}}$,${ω}_{2}=\sqrt{\frac{GM}{{{r}_{2}}^{3}}}$
求得t=$\frac{2πn}{\sqrt{\frac{GM}{{{r}_{1}}^{3}}}-\sqrt{\frac{GM}{{{r}_{2}}^{3}}}}$(n=1,2,3…).
答:再经过$\frac{2πn}{\sqrt{\frac{GM}{{{r}_{1}}^{3}}}-\sqrt{\frac{GM}{{{r}_{2}}^{3}}}}$(n=1,2,3…)时间两行星距离又最近.
点评 本题根据处理卫星问题的基本思路:万有引力等于向心力的基础上,抓住圆周运动的周期性,运用数学知识求解时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
 质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )| A. | 小车重力所做的功是mgh | B. | 合力对小车做的功是$\frac{m{v}^{2}}{2}$+mgh | ||
| C. | 阻力对小车做的功是$\frac{m{v}^{2}}{2}$+mgh-Fs | D. | 推力对小车做的功是Fs-mgh |
17.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所做科学贡献的叙述中,正确的说法是( )
| A. | 英国物理学家卡文迪许用实验的方法测出万有引力常量G | |
| B. | 牛顿通过计算首先发现了海王星和冥王星 | |
| C. | 哥白尼首先提出了“地心说” | |
| D. | 开普勒经过多年的天文观测和记录,提出了“日心说”的观点 |
14.下列说法正确的是( )
| A. | 物体速度发生变化,动能一定变化 | |
| B. | 物体的动能发生变化,速度一定变化 | |
| C. | 物体的合外力做了功,动能一定减小 | |
| D. | 物体动能增大时,势能一定减小 |
13. 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球,从距离水平地面为H的管口D处静止释放,最后能够从A端水平抛出落到地面上.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球,从距离水平地面为H的管口D处静止释放,最后能够从A端水平抛出落到地面上.下列说法正确的是( )
 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球,从距离水平地面为H的管口D处静止释放,最后能够从A端水平抛出落到地面上.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球,从距离水平地面为H的管口D处静止释放,最后能够从A端水平抛出落到地面上.下列说法正确的是( )| A. | 小球落到地面时相对于A点的水平位移值为2$\sqrt{RH-2{R}^{2}}$ | |
| B. | 小球落到地面时相对于A点的水平位移值为$\sqrt{2RH-4{R}^{2}}$ | |
| C. | 小球能从细管A端水平抛出的条件是H>2R | |
| D. | 小球能从细管A端水平抛出的最小高度Hmin=$\frac{5}{2}$R |
14. 奥地利著名极限运动员鲍姆加特纳曾经从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中,沿竖直方向运动的v-t图象如图所示,则下列说法中不正确的是( )
奥地利著名极限运动员鲍姆加特纳曾经从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中,沿竖直方向运动的v-t图象如图所示,则下列说法中不正确的是( )
 奥地利著名极限运动员鲍姆加特纳曾经从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中,沿竖直方向运动的v-t图象如图所示,则下列说法中不正确的是( )
奥地利著名极限运动员鲍姆加特纳曾经从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中,沿竖直方向运动的v-t图象如图所示,则下列说法中不正确的是( )| A. | 0-t1内运动员和所有装备整体所受重力大于空气阻力,且空气阻力不断增大 | |
| B. | t1秒末运动员打开降落伞后,有“心提到嗓子眼儿”的感觉,之后这种难受程度会逐渐减弱 | |
| C. | t1秒末到t2秒末运动员竖直方向的加速度方向向下,大小在逐渐增大 | |
| D. | t2秒后运动员保持匀速下落 |
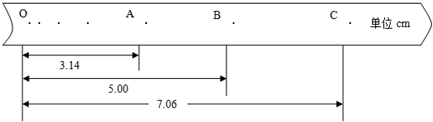
 如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0.
如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0. 如图所示,半径为R的半圆形轨道竖直放置,左右两端高度相同,质量为m的小球从端点A由静止开始运动,通过最低点B时对轨道压力大小为2mg,求:
如图所示,半径为R的半圆形轨道竖直放置,左右两端高度相同,质量为m的小球从端点A由静止开始运动,通过最低点B时对轨道压力大小为2mg,求: