题目内容
6.电子、质子和a粒子从静止开始,在相同的电压加速后,垂直电场线进入同一匀强电场中,则下列说法错误的是( )| A. | 最后离开电场时,a粒子偏角最大 | B. | 电子通过匀强电场的时间最短 | ||
| C. | 最后离开电场时,质子速率最大 | D. | 最后离开电场时,质子动能最大 |
分析 带电粒子经加速电场加速时,由动能定理求得获得的速度,进入偏转时,粒子做类平抛运动,运用运动的分解法得到偏转角和偏转量y的表达式,进行比较.求出速度的表达式,进行比较即可;根据动能定理电场经过加速电场后的速度关系,在偏转电场中沿垂直于电场方向的位移相等,即可求得结论.
解答 解:A、加速电场中:由动能定理得:
qU1=$\frac{1}{2}$m${v}_{0}^{2}$
在偏转电场中:
平行于极板方向:L=v0t
垂直于极板方向:vy=at,a=$\frac{qE}{m}$=$\frac{q{U}_{2}}{md}$
粒子的偏转角:tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{at}{{v}_{0}}$
联立解得:tanθ=$\frac{{U}_{2}L}{2{U}_{1}d}$,则知偏转角与电荷的质量和电量无关,所以三个粒子的偏转角相等,故A错误;
B、粒子通过匀强电场的时间 t=$\frac{L}{{v}_{0}}$=$\frac{L}{\sqrt{\frac{2q{U}_{1}}{m}}}$,电子的比荷最大,时间最短,故B正确.
CD、粒子的偏转量:y=$\frac{1}{2}a{t}^{2}$
联立解得:y=$\frac{{U}_{2}{L}^{2}}{4{U}_{1}d}$,偏移量与电荷的质量和电量无关,所以偏转电场对粒子做的功:
W=qE•y=q$\frac{{U}_{2}}{d}$•$\frac{{U}_{2}{L}^{2}}{4{U}_{1}d}$=$\frac{q{U}_{2}^{2}{L}^{2}}{4{U}_{1}{d}^{2}}$,与粒子所带的电量成正比,最后离开电场时的动能 Ek=qU1+W∝q,所以最后离开电场时α粒子的动能最大.故D错误;
由Ek=$\frac{1}{2}m{v}^{2}$,得离开电场时的速率:v=$\sqrt{\frac{2(q{U}_{1}+W)}{m}}$,与粒子比荷的平方根成正比.所以最后离开电场时电子的速率最大.故C错误;
本题选错误的,故选:ACD
点评 本题是带电粒子在匀强电场中做类平抛运动的类型,电子先经加速电场加速,后经偏转电场偏转,得到的结论:偏转量与电荷的质量和电量无关.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 质点始终向同一方向运动 | |
| B. | 在运动过程中,质点运动方向发生2次变化 | |
| C. | 0-t1s内做加速直线运动 | |
| D. | t1-t3 s内做减速直线运动 |
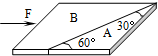 将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )
将某种材料的长方体锯成A、B两块放在水平桌面上,并紧靠在一起,如图所示,物体A的角度如图中所示.现用水平方向的力F推物体,使A、B保持矩形整体沿力F方向匀速运动,则( )| A. | 物体A在水平方向受两个力作用,合力为零 | |
| B. | 作用于A的摩擦力不止一个 | |
| C. | 物体B对A的压力大小等于桌面对A的摩擦力大小 | |
| D. | 物体B受五个力作用 |
 如图所示,一名骑独轮车的杂技演员在空中钢丝绳上表演,如果演员和独轮车的总质量为80kg,两侧的钢丝绳互成120°夹角,则钢丝绳的张力大小为(不计钢丝绳的重力,取g=10m/s2)( )
如图所示,一名骑独轮车的杂技演员在空中钢丝绳上表演,如果演员和独轮车的总质量为80kg,两侧的钢丝绳互成120°夹角,则钢丝绳的张力大小为(不计钢丝绳的重力,取g=10m/s2)( )| A. | 400N | B. | 600N | C. | 800N | D. | 1 600N |
| A. | 速度大小一定改变了 | B. | 速度方向一定改变了 | ||
| C. | 速度一定变化了 | D. | 加速度可能为零 |
 如图:物体m由静止开始沿倾角为α的光滑斜面下滑.已知斜面高为H,求
如图:物体m由静止开始沿倾角为α的光滑斜面下滑.已知斜面高为H,求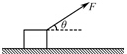 质量m=0.78kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=4.5N,方向与水平方向成θ=37°角斜向上,如图所示.3s末撤去此拉力时,木块已滑行的距离s0=9m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求:
质量m=0.78kg的木块静止于水平面上,现在恒力F作用下做匀加速直线运动,已知恒力大小F=4.5N,方向与水平方向成θ=37°角斜向上,如图所示.3s末撤去此拉力时,木块已滑行的距离s0=9m,(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.)求: 如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形的平面已知图片里的三点电势(A点电势10V,B点电势2V,C点电势4V)用作图法在图中画出过C点的等势面和过A的电场线.
如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形的平面已知图片里的三点电势(A点电势10V,B点电势2V,C点电势4V)用作图法在图中画出过C点的等势面和过A的电场线. 如图所示,两水平放置的平行金属板与电源相连,其间一带电液滴恰好静止平衡.若将两板板之间的距离由d变为$\frac{3d}{2}$,液滴的加速度a=5m/s2.
如图所示,两水平放置的平行金属板与电源相连,其间一带电液滴恰好静止平衡.若将两板板之间的距离由d变为$\frac{3d}{2}$,液滴的加速度a=5m/s2.