题目内容
1.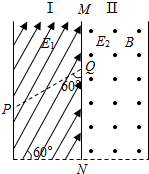 如图所示,在Ⅰ区里有与水平方向成60°角的匀强电场E1,宽度为d,在Ⅱ区里有垂直于平面向外的匀强磁场和竖直方向的电场E2,宽度也为d,一带电量为q、质量为m的微粒自图中P点由静止释放后沿虚线做直线运动进入Ⅱ区的磁场,已知PQ与中间边界MN的夹角是60°,若粒子进入Ⅱ区后再做匀速圆周运动还能回到MN边界上.重力加速度为g,Ⅰ区和Ⅱ区的场在竖直方向足够长,d、m、q已知,求:
如图所示,在Ⅰ区里有与水平方向成60°角的匀强电场E1,宽度为d,在Ⅱ区里有垂直于平面向外的匀强磁场和竖直方向的电场E2,宽度也为d,一带电量为q、质量为m的微粒自图中P点由静止释放后沿虚线做直线运动进入Ⅱ区的磁场,已知PQ与中间边界MN的夹角是60°,若粒子进入Ⅱ区后再做匀速圆周运动还能回到MN边界上.重力加速度为g,Ⅰ区和Ⅱ区的场在竖直方向足够长,d、m、q已知,求:(1)微粒带何种电荷,Ⅰ区和Ⅱ区电场E1和E2的大小的比值及E2方向;
(2)若微粒能再次回到MN边界,Ⅱ区磁感应强度B的范围;
(3)微粒从开始运动到第二次到达MN的最长时间.
分析 (1)微粒在Ⅰ区受到重力和电场力作用而做初速度为零的匀加速直线运动,画出其受力示意图,求解电场强度E1的大小.在Ⅱ区微粒做匀速圆周运动,重力与电场力平衡,由此列式求解E2的大小,并确定E2方向.即可求解E1和E2的大小的比值.
(2)若微粒恰能再次回到MN边界,其轨迹与磁场Ⅱ右边界相切,画出轨迹,求出轨迹半径,由牛顿第二定律求出磁感应强度的最小值,从而得到其范围.
(3)在Ⅰ区中,由运动学公式求解时间.在Ⅱ区,根据轨迹的圆心角求解时间,从而得到总时间.
解答 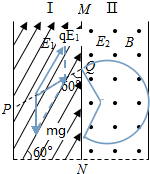
 解:(1)微粒在Ⅰ区受到重力和电场力作用而做初速度为零的匀加速直线运动,受力示意图如图,其合力沿PQ方向,可知微粒带正电.
解:(1)微粒在Ⅰ区受到重力和电场力作用而做初速度为零的匀加速直线运动,受力示意图如图,其合力沿PQ方向,可知微粒带正电.
由几何关系得:qE1=2mgcos30°
可得 E1=$\frac{\sqrt{3}mg}{q}$
在Ⅱ区微粒做匀速圆周运动,重力与电场力平衡,有 qE2=mg
可得 E2=$\frac{mg}{q}$,方向竖直向上.
故$\frac{{E}_{1}}{{E}_{2}}$=$\sqrt{3}$
(2)在Ⅰ区中,由几何关系可知,微粒的合外力F合=mg
根据动能定理得 F合$\frac{d}{sin60°}$=$\frac{1}{2}m{v}^{2}$
解得 v=2$\sqrt{\frac{\sqrt{3}gd}{3}}$
若微粒恰能再次回到MN边界,其轨迹与磁场Ⅱ右边界相切,画出轨迹如图,设轨迹半径为r,则
r+rsin30°=d
得 r=$\frac{2}{3}$d
由qvB=m$\frac{{v}^{2}}{r}$得 B=$\frac{m\sqrt{3\sqrt{3}gd}}{qd}$
故,Ⅱ区磁感应强度B的范围 B>$\frac{m\sqrt{3\sqrt{3}gd}}{qd}$.
(3)设微粒在Ⅰ区和Ⅱ区运动时间分别为t1和t2.
则 $\frac{d}{sin60°}$=$\frac{v{t}_{1}}{2}$,得t1=2$\sqrt{\frac{d}{g}}$
t2=$\frac{240°}{360°}$T
而周期 T=$\frac{2πm}{qB}$
联立得 t2=$\frac{4π}{3\sqrt{3\sqrt{3}}}$$\sqrt{\frac{d}{g}}$
故总时间 t=t1+t2=(2+$\frac{4π}{3\sqrt{3\sqrt{3}}}$)$\sqrt{\frac{d}{g}}$
答:
(1)微粒带正电荷,Ⅰ区和Ⅱ区电场E1和E2的大小的比值为$\sqrt{3}$,E2方向竖直向上;
(2)若微粒能再次回到MN边界,Ⅱ区磁感应强度B的范围 B>$\frac{m\sqrt{3\sqrt{3}gd}}{qd}$;
(3)微粒从开始运动到第二次到达MN的最长时间为(2+$\frac{4π}{3\sqrt{3\sqrt{3}}}$)$\sqrt{\frac{d}{g}}$.
点评 本题要掌握受力分析的方法,掌握受力平衡状态方程,理解力的平行四边形定则与牛顿第二定律的应用,注意几何关系在本题的运用.

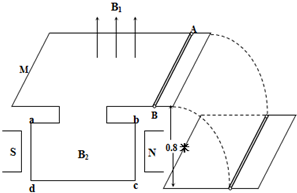
 如图所示,匀强磁场的磁感应强度B为0.5T,其方向垂直于倾角θ为30°的斜面向上.绝缘斜面上固定有∧形状的光滑金属导轨MON(电阻忽略不计),MO和NO长度均为2.5m,MN连线水平,MN间距离为3m,以O为原点,在垂直于MN的方向上建立一维坐标系Ox.一根粗细均匀的金属杆PQ,质量为m=0.1kg,长度d=3m,电阻为3Ω且均匀分布.在沿+x方向的拉力F作用下从O点静止开始以2.5m/s2的加速度做匀加速运动,取g=10m/s2,则金属杆PQ运动到x=0.8m处时,PQ间的电势差为UPQ,拉力为F,则有( )
如图所示,匀强磁场的磁感应强度B为0.5T,其方向垂直于倾角θ为30°的斜面向上.绝缘斜面上固定有∧形状的光滑金属导轨MON(电阻忽略不计),MO和NO长度均为2.5m,MN连线水平,MN间距离为3m,以O为原点,在垂直于MN的方向上建立一维坐标系Ox.一根粗细均匀的金属杆PQ,质量为m=0.1kg,长度d=3m,电阻为3Ω且均匀分布.在沿+x方向的拉力F作用下从O点静止开始以2.5m/s2的加速度做匀加速运动,取g=10m/s2,则金属杆PQ运动到x=0.8m处时,PQ间的电势差为UPQ,拉力为F,则有( )| A. | UPQ=-3V | B. | UPQ=-1.8V | C. | F=1.35N | D. | F=0.85N |
| A. | 周期越小 | B. | 环绕速度越小 | C. | 角速度越小 | D. | 加速度越小 |
| A. | 书受的重力就是桌面受到的压力 | |
| B. | 书受到了支持力是因为桌面产生了形变 | |
| C. | 书受到了支持力是因为书产生了形变 | |
| D. | 桌面受到的压力和桌面给书的支持力不是桌面与书之间的相互作用 |