题目内容
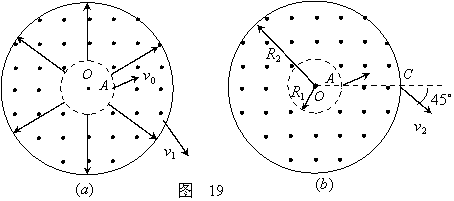
如图19(a)所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
(1)已知粒子从外圆上以速度v1射出,求粒子在A点的初速度v0的大小。
(2)若撤去电场,如图19(b),已知粒子从OA延长线与外圆的交点C以速度v2射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
(3)在图19(b)中,若粒子从A点进入磁场,速度大小为v3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?

解:
(1)电、磁场都存在时,只有电场力对带电粒子做功,由动能定理
![]() ①(3分)
①(3分)
得![]() ②(3分)
②(3分)
(2)由牛顿第二定律 ![]() ③(2分)
③(2分)
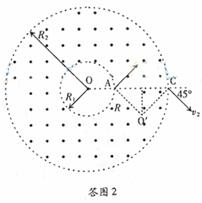
如答图2,由几何关系粒子运动轨迹的圆心![]() 和半径R,则
和半径R,则
![]() ④(2分)
④(2分)
联立③④得磁感应强度大小![]() ⑤(2分)
⑤(2分)
粒子在磁场中做匀速圆周运动的周期![]() ⑥(2分)
⑥(2分)
由几何关系确定粒子在磁场中运动的时间![]() ⑦(1分)
⑦(1分)
由④⑥⑦式,得 ![]() ⑧(1分)
⑧(1分)
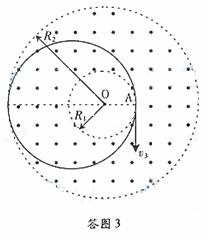
(3)如答图3,为使粒子射出,则粒子在磁场内的运动半径应大于过A点的最大内切圆半径,该半径为
![]() ⑨(2分)
⑨(2分)
由③⑨,得磁感应强度应小于![]() ⑾(2分)
⑾(2分)

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
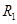 和
和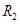 的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,
的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,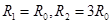 ,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。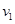 射出,求粒子在A点的初速度
射出,求粒子在A点的初速度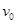 的大小
的大小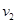 射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间
射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间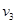 ,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?
,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?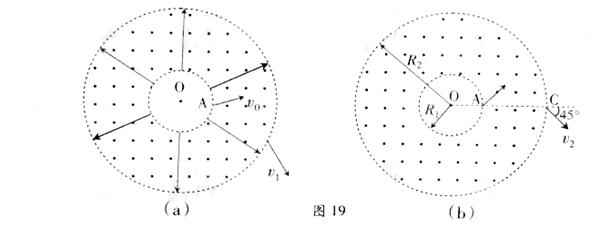
 和
和 的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,
的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量, ,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。 射出,求粒子在A点的初速度
射出,求粒子在A点的初速度 的大小
的大小 射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间
射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间 ,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?
,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?