题目内容
【题目】如图所示，质量为m的滑块从 h高处的a点沿圆弧轨道ab滑入水平轨道bc ， 滑块与轨道的动摩擦因素相同．滑块在a、c两点时的速度大小均为v ， ab弧长与bc长 度相等．空气阻力不计，则滑块从a 到c 的运 动过程中（ ）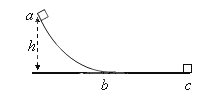 
A.小球的动能始终保持不变
B.小球在bc过程克服阻力做的功一定等于mgh/2
C.小球经b点时的速度大于 
D.小球经b点时的速度等于 
【答案】C
【解析】解答：滑块在a、c两点时的速度大小均为v ， 知滑块先加速后减速．动能先增加后减小．故A错误；对全程运用动能定理得，mgh-Wf=0，全程克服阻力做功等于mgh ， 因为ab段所受的支持力小于重力，所以所受的摩擦力与bc段不等，克服摩擦力做功不等，且在斜面上克服阻力做功小于在水平面克服阻力做功，则小球在bc过程克服阻力做的功不等于 
．故B错误；根据动能定理得：mgh-Wf′＝ 
，因为Wf′< ，所以vb> 
．故C正确，D错误 故选：C
分析：注意全程动能定理的应用
【考点精析】解答此题的关键在于理解动能定理的理解的相关知识，掌握动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的.但它也适用于变力及物体作曲线运动的情况；功和动能都是标量，不能利用矢量法则分解，故动能定理无分量式．
练习册系列答案
寒假学与练系列答案
相关题目
