Question

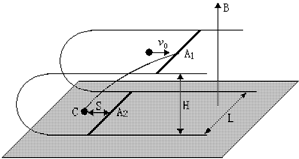（2006?广东）如图所示，在磁感应强度大小为B、方向垂直向上的匀强磁场中，有一上、下两层均与水平面平行的“U”型光滑金属导轨，在导轨面上各放一根完全相同的质量为m的匀质金属杆A₁和A₂，开始时两根金属杆位于同一竖起面内且杆与轨道垂直．设两导轨面相距为H，导轨宽为L，导轨足够长且电阻不计，金属杆单位长度的电阻为r．现有一质量为

m

2

的不带电小球以水平向右的速度v₀撞击杆A₁的中点，撞击后小球反弹落到下层面上的C点．C点与杆A₂初始位置相距为S．求：
（1）回路内感应电流的最大值；
（2）整个运动过程中感应电流最多产生了多少热量；
（3）当杆A₂与杆A₁的速度比为1：3时，A₂受到的安培力大小．

Answer 1

分析：金属杆A₁、A₂两杆在同一个金属U形导轨上都做变速运动，运动方向相同（都向右），同一时刻两杆都切割磁感线产生感应电动势，两个感应电动势在空间中的方向相同（都向外），但两个感应电动势在回路中的方向相反，所以总电动势是这两个电动势之差，即E=BL（v₁-v₂），电流是I=

BL(v1-v2)

R

，方向为金属杆A₁中感应电流的方向，因为A₁比A₂产生的感应电动势大，安培力是F=

B2L2(v1-v2)

R

，方向都和速度方向相反（都向左）．
根据平抛运动规律、动量守恒定律、能量守恒定律解决问题．

解答：解：设撞击后小球反弹的速度为v₁，金属杆A1的速度为v₀₁，根据动量守恒定律，

1

2

mv₀=

1

2

m（-v₁）+mv₀₁，①
 根据平抛运动的分解，有
 　s=v₁t，H=

1

2

gt²
 　由以上2式解得v₁=s

g 2H

       ②
 　②代入①得v₀₁=

1

2

（v₀+s

g 2H

）      ③
 　回路内感应电动势的最大值为E_m=BLv₀₁，电阻为R=2Lr，
所以回路内感应电流的最大值为I_m=

B(v0+s g 2H )

4r

．        ④
 （2）因为在安培力的作用下，金属杆A₁做减速运动，金属杆A₂做加速运动，当两杆速度大小相等时，回路内感应电流为0，根据能量守恒定律，

1

2

mv₀₁²=Q+

1

2

?2mv²    ⑤
其中v是两杆速度大小相等时的速度，根据动量守恒定律，
mv₀₁=2mv，所以v=

1

2

v₀₁，代入⑤式得
Q=

1

16

m（v₀+s

g 2H

）²    ⑥
（3）设金属杆A₁、A₂速度大小分别为v₁、v₂，根据动量守恒定律，
mv₀₁=mv1+mv₂，又

v1

v2

=

3

1

，所以
v₁=

3

4

v₀₁，v₂=

1

4

v₀₁．
金属杆A₁、A₂速度方向都向右，根据右手定则判断A₁、A₂产生的感应电动势在回路中方向相反，
所以感应电动势为E=BL（v₁-v₂），电流为I=

E

2Lr

，安培力为F=BIL，
所以A₂受到的安培力大小为F=

B2L

8r

（v₀+s

g 2H

）．
当然A₁受到的安培力大小也如此，只不过方向相反．
 答案：（1）回路内感应电流的最大值为

B(v0+s g 2H )

4r

；
（2）整个运动过程中感应电流最多产生热量为

1

16

m（v₀+s

g 2H

）²；
（3）当杆A₂与杆A₁的速度比为1：3时，A₂受到的安培力大小为

B2L

8r

（v0+s

g 2H

）．

点评：注重金属杆A₁、A₂两杆的运动过程分析，清楚同一时刻两杆都切割磁感线产生感应电动势时，根据两个感应电动势在回路中的方向会求出电路中总的感应电动势．