题目内容
 如图所示的皮带传动装置中,甲、乙、丙三轮的轴均为水平轴,其中甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )
如图所示的皮带传动装置中,甲、乙、丙三轮的轴均为水平轴,其中甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )分析:甲、乙两轮是皮带传动,皮带传动的特点是皮带和轮子接触点的线速度的大小相同,乙、丙两轮是轴传动,轴传动的特点是角速度相同.然后根据线速度、角速度、半径之间的关系即可求解.
解答:解:A、由于甲、乙两轮是皮带传动,皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同,
故vA=vB
∴vA:vB=1:1
由角速度和线速度的关系式v=ωR可得
ωA:ωB=RB:RA=1:2
而向心加速度an=
,
得向心加速度与半径成反比,
即A、B两点向心加速度大小之比1:2;故AC均错误;
B、由于乙、丙两轮共轴,故两轮角速度相同,
即ωB=ωC,
ωA:ωB:ωC=1:2:2
所以B、C两点的角速度大小之比为1:1;故B错误;
D、而向心加速度an=
,
得向心加速度与半径成反比,
即A、C两点的向心加速度大小之比为1:4;故D正确;
故选D
故vA=vB
∴vA:vB=1:1
由角速度和线速度的关系式v=ωR可得
ωA:ωB=RB:RA=1:2
而向心加速度an=
| v2 |
| R |
得向心加速度与半径成反比,
即A、B两点向心加速度大小之比1:2;故AC均错误;
B、由于乙、丙两轮共轴,故两轮角速度相同,
即ωB=ωC,
ωA:ωB:ωC=1:2:2
所以B、C两点的角速度大小之比为1:1;故B错误;
D、而向心加速度an=
| v2 |
| R |
得向心加速度与半径成反比,
即A、C两点的向心加速度大小之比为1:4;故D正确;
故选D
点评:解决传动类问题要分清是摩擦传动(包括皮带传动,链传动,齿轮传动,线速度大小相同)还是轴传动(角速度相同).

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=3RB,则三质点的向心加速度之比aA:aB:aC等于( )
如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=3RB,则三质点的向心加速度之比aA:aB:aC等于( )| A、9:3:1 | B、3:1:3 | C、1:3:9 | D、9:1:9 |
 (2012?徐汇区一模)如图所示的皮带传动装置中,A、B两轮半径分别为rA和rB,已知rA<rB,且皮带不打滑.在传动过程中,下列说法正确的是( )
(2012?徐汇区一模)如图所示的皮带传动装置中,A、B两轮半径分别为rA和rB,已知rA<rB,且皮带不打滑.在传动过程中,下列说法正确的是( )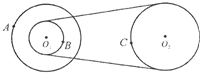 如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=2RB岛,若传动过程中皮带不打滑,则下列说法正确的是( )
如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=2RB岛,若传动过程中皮带不打滑,则下列说法正确的是( ) (2006?济南模拟)如图所示的皮带传动装置中,轮B和C同轴,A、B、C分别是三个轮边缘的质点,且其半径RA=RC=2RB,则三质点的向心加速度之比aA:aB:aC等于( )
(2006?济南模拟)如图所示的皮带传动装置中,轮B和C同轴,A、B、C分别是三个轮边缘的质点,且其半径RA=RC=2RB,则三质点的向心加速度之比aA:aB:aC等于( ) 如图所示的皮带传动装置中,图中A、B、C三点的半径关系为RA=2RB=2RC,设皮带不打滑,则有VA:VB:VC=
如图所示的皮带传动装置中,图中A、B、C三点的半径关系为RA=2RB=2RC,设皮带不打滑,则有VA:VB:VC=