题目内容
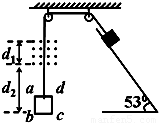
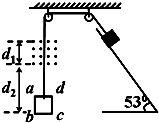如图，一边长L=0.4m、质量m1=0.2kg、电阻R=0.1Ω的正方形导体线框abcd，与一质量为m2=1.0kg的物块通过轻质细线跨过两定滑轮相连．磁感应强度B=1.0T，磁场宽度d1=0.8m，开始时bc边距磁场下边界为d2=1.0m，物块放在倾角θ=53°的斜面上，物块与斜面间的动摩擦因数为μ=| 1 | 3 |
（1）线框ad边从磁场上边缘穿出时速度的大小；
（2）线框ad边刚刚进入磁场时的动能；
（3）线框从开始运动到全部穿出磁场的过程中产生的焦耳热．
分析：根据物体运动状态和受力分析，结合安培力公式求出线框ad边从磁场上边缘穿出时速度的大小
对整体运动动能定理，求出线框ad边刚刚进入磁场时速度，再求出动能．
对整体运用能量守恒求出产生的焦耳热．
对整体运动动能定理，求出线框ad边刚刚进入磁场时速度，再求出动能．
对整体运用能量守恒求出产生的焦耳热．
解答：解：（1）设ad边从磁场上边缘穿出时速度为 v1，物块此后也匀速运动
对m2：T+μm2gcos53°=m2gsin53°
求得：T=6 N
对m1：T-m1g-F安=0
F安=BIL
解得：v1=2.5m/s
（2）设线框ad边刚刚进入磁场时，速度为v2，对整体有
（m2gsin53°-μm2gcos53°）（d2-L）-m1g（d2-L）=
（m1+m2）v22
解得：v2=2.5m/s
∴Ek=
m1v22=0.4J
（3）从开始运动到bc边离开磁场，对整体有
（m2gsin53°-μm2gcos53°）（d1+d2）-m1g（d1+d2）-W安=
（m1+m2）v12
对线框有Q=W安
解得：Q=3.45 J．
答：（1）线框ad边从磁场上边缘穿出时速度的大小是2.5m/s；
（2）线框ad边刚刚进入磁场时的动能是0.4J；
（3）线框从开始运动到全部穿出磁场的过程中产生的焦耳热是3.45 J．
对m2：T+μm2gcos53°=m2gsin53°
求得：T=6 N
对m1：T-m1g-F安=0
F安=BIL
解得：v1=2.5m/s
（2）设线框ad边刚刚进入磁场时，速度为v2，对整体有
（m2gsin53°-μm2gcos53°）（d2-L）-m1g（d2-L）=
| 1 |
| 2 |
解得：v2=2.5m/s
∴Ek=
| 1 |
| 2 |
（3）从开始运动到bc边离开磁场，对整体有
（m2gsin53°-μm2gcos53°）（d1+d2）-m1g（d1+d2）-W安=
| 1 |
| 2 |
对线框有Q=W安
解得：Q=3.45 J．
答：（1）线框ad边从磁场上边缘穿出时速度的大小是2.5m/s；
（2）线框ad边刚刚进入磁场时的动能是0.4J；
（3）线框从开始运动到全部穿出磁场的过程中产生的焦耳热是3.45 J．
点评：本题考查了电磁感应与力学和功能关系的综合，对于这类问题要正确受力分析，尤其是正确分析安培力的情况，然后分析清楚运动情况．
练习册系列答案
优学名师名题系列答案
相关题目
的正方形导体线框abcd，与一质量为m2＝1.0 kg的物块通过轻质细线跨过两定滑轮相连．磁感应强度B＝1.0 T，磁场宽度d1＝0.8 m，开始时bc边距磁场下边界为d2＝1.0 m，物块放在倾角θ＝53o的斜面上，物块与斜面间的动摩擦因数为m
＝
．现将物块由静止释放，经过一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动，已知sin53o＝0.8，cos53o＝0.6取g＝10 m/s2．求：
的正方形导体线框abcd，与一质量为m2＝1.0kg的物块通过轻质细线跨过两定滑轮相连。磁感应强度B＝1.0T，磁场宽度d1＝0.8m，开始时bc边距磁场下边界为d2＝1.0m，物块放在倾角θ＝53º的斜面上，物块与斜面间的动摩擦因数为m＝。现将物块由静止释放，经过一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动，已知sin53º＝0.8，cos53º＝0.6取g＝10m/s2。求：
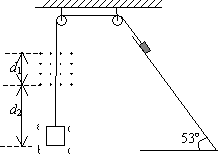
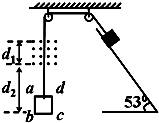
．现将物块由静止释放，经过一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动，已知sin53°=0.8，cos53°=0.6，取g=10m/s2．求：