题目内容
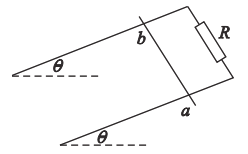
【题目】如图所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角α，导轨电阻不计．磁感应强度为B的匀强磁场垂直导轨平面向上，长为L的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为m、电阻为R。定值电阻的阻值也为R，重力加速度为g，闭合开关S，现将金属棒由静止释放。
（1）求金属棒下滑的最大速度va；
（2）金属棒从静止开始下滑距离为s0时速度恰好达到最大；
①求该过程通过金属棒的电量q；
②a.求该过程中金属棒的生热Q；
b.试证明该过程中任意时刻金属棒克服安培力的功率都等于全电路的生热功率。
（3）金属棒从静止开始下滑距离为s0时速度恰好达到最大，求该过程中金属棒所用的时间t。
【答案】（1）
（2）①
②a. 
b.见解析；（3）
【解析】
（1）当金属棒到达最大速度时，由平衡知识可知：
解得
（2）①由
；
；
；
解得
②a.由能量关系可知：
b.设某一时刻金属棒的速度为v，则安培力的功率：
；
电动势E=BLv，则全电路的生热功率
，
即该过程中任意时刻金属棒克服安培力的功率都等于全电路的生热功率，问题得证。
（3）由动量定理可知：
，而
联立解得：
练习册系列答案
相关题目
