题目内容
7.取水平地面为重力势能零点,一物块从某一高度水平抛出,在抛出点其动能与重力势能恰好相等,不计空气阻力,该物块落地时的速度方向与水平方向的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
分析 根据机械能守恒定律,以及已知条件:抛出时动能与重力势能恰好相等,分别列式即可求出落地时速度与水平速度的关系,从而求出物块落地时的速度方向与水平方向的夹角.
解答 解:设抛出时物体的初速度为v0,高度为h,物块落地时的速度大小为v,方向与水平方向的夹角为α.根据机械能守恒定律得:
$\frac{1}{2}m{v}_{0}^{2}$+mgh=$\frac{1}{2}m{v}^{2}$,
据题有:$\frac{1}{2}m{v}_{0}^{2}$=mgh,
联立解得:v=$\sqrt{2}{v}_{0}$,
则cosα=$\frac{{v}_{0}}{v}$=$\frac{\sqrt{2}}{2}$,
得:α=$\frac{π}{4}$.
故选:C.
点评 解决本题的关键会熟练运用机械能守恒定律处理平抛运动,并要掌握平抛运动的研究方法:运动的分解.

练习册系列答案
相关题目
8. 如图所示的电路中,电源内阻不可忽略,当滑动变阻器滑片处在某一位置时,安培表的读数为I=0.5A,电压表V1的读数为U1=1V,电压表V2的读数为U2=2V.则左右任意移动滑动变阻器的滑片后,三个电表可能得到的读数是( )
如图所示的电路中,电源内阻不可忽略,当滑动变阻器滑片处在某一位置时,安培表的读数为I=0.5A,电压表V1的读数为U1=1V,电压表V2的读数为U2=2V.则左右任意移动滑动变阻器的滑片后,三个电表可能得到的读数是( )
 如图所示的电路中,电源内阻不可忽略,当滑动变阻器滑片处在某一位置时,安培表的读数为I=0.5A,电压表V1的读数为U1=1V,电压表V2的读数为U2=2V.则左右任意移动滑动变阻器的滑片后,三个电表可能得到的读数是( )
如图所示的电路中,电源内阻不可忽略,当滑动变阻器滑片处在某一位置时,安培表的读数为I=0.5A,电压表V1的读数为U1=1V,电压表V2的读数为U2=2V.则左右任意移动滑动变阻器的滑片后,三个电表可能得到的读数是( )| A. | I=2A U1=2V U2=0V | B. | I=1A U1=1.6V U2=3V | ||
| C. | I=0.3A U1=0.9V U2=2.1V | D. | I=0.2A U1=0.8V U2=2.4V |
2.汽车在平直公路上行驶,所受阻力为f,最大功率为P,在它起动后作匀加速直线运动阶段中,下面说法中正确的是( )
| A. | 牵引力逐渐增大,发动机功率不变 | B. | 牵引力不变,发动机功率逐渐增大 | ||
| C. | 功率不可能增大到P | D. | 速度不可能增大到$\frac{P}{f}$ |
12.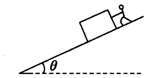 在倾角为30°的斜面上,某人用平行于斜面的力把原来静止于斜面上的质量为2kg的物体沿斜面向下推了2m的距离,并使物体获得1m/s的速度,已知物体与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,(g取10m/s2)则在这个过程中( )
在倾角为30°的斜面上,某人用平行于斜面的力把原来静止于斜面上的质量为2kg的物体沿斜面向下推了2m的距离,并使物体获得1m/s的速度,已知物体与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,(g取10m/s2)则在这个过程中( )
 在倾角为30°的斜面上,某人用平行于斜面的力把原来静止于斜面上的质量为2kg的物体沿斜面向下推了2m的距离,并使物体获得1m/s的速度,已知物体与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,(g取10m/s2)则在这个过程中( )
在倾角为30°的斜面上,某人用平行于斜面的力把原来静止于斜面上的质量为2kg的物体沿斜面向下推了2m的距离,并使物体获得1m/s的速度,已知物体与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$,(g取10m/s2)则在这个过程中( )| A. | 人对物体做功21J | B. | 合外力对物体做功1J | ||
| C. | 物体克服摩擦力做功20J | D. | 物体机械能减少了21J |
19.关于电容器,下列说法中正确的是( )
| A. | 电容器就是电源 | |
| B. | 电容器是描述电容器储存电荷本领大小的物理量 | |
| C. | 电容器极板的正对面积越大,极板间距离越大,电容器的电容就越大 | |
| D. | 使电容器带电的过程叫充电 |
 如图一闭合三角形导线框ABC,∠ABC=120°,AB=BC=1m,放在磁感应强度为2T的匀强磁场中,磁场垂直于线框平面,若在线框中通以I=1A的电流,则AB与BC所受磁场力的合力大小为3.46N,整个线框所受磁场力的合力大小为0N.
如图一闭合三角形导线框ABC,∠ABC=120°,AB=BC=1m,放在磁感应强度为2T的匀强磁场中,磁场垂直于线框平面,若在线框中通以I=1A的电流,则AB与BC所受磁场力的合力大小为3.46N,整个线框所受磁场力的合力大小为0N.