题目内容
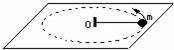
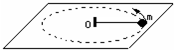
如图所示，长为L细绳一端固定于O点，另一端系一质量为m的小球并让小球以速度v在光滑水平面内做匀速圆周运动求：（1）小球运动的角速度
（2）小球受到绳子的拉力大小．
分析：（1）小球在光滑水平面内做匀速圆周运动，由v=ωL求角速度ω．
（2）小球做匀速圆周运动时，由绳子的拉力提供向心力，根据牛顿第二定律求绳子的拉力．
（2）小球做匀速圆周运动时，由绳子的拉力提供向心力，根据牛顿第二定律求绳子的拉力．
解答：解：（1）由v=ωL得：小球运动的角速度ω=
．
（2）小球做匀速圆周运动时，由绳子的拉力提供向心力，根据牛顿第二定律得：
绳子的拉力F=m
答：
（1）小球运动的角速度为
（2）小球受到绳子的拉力大小是m
．
| v |
| L |
（2）小球做匀速圆周运动时，由绳子的拉力提供向心力，根据牛顿第二定律得：
绳子的拉力F=m
| v2 |
| L |
答：
（1）小球运动的角速度为
| v |
| L |
（2）小球受到绳子的拉力大小是m
| v2 |
| L |
点评：本题关键要掌握匀速圆周运动的角速度与线速度的关系公式v=ωr，分析向心力的来源，比较简单．
练习册系列答案
相关题目
如图所示，长为L的细绳，一端系着一只小球，另一端悬于O点，将小球由图示位置由静止释放，当摆到O点正下方时，绳被小钉挡住．当钉子分别处于图中A、B、C三个不同位置时，小球继续摆的最大高度分别为h1、h2、h3，则（ ）
如图所示，长为L的细绳竖直悬挂着一质量为2m的小球A，恰好紧挨着放置在水平光滑桌面右端质量为m的物块B．现保持细绳绷直，把小球向左上方拉至细绳与竖直方向成600的位置，然后释放小球．小球到达最低点时恰好与物块发生碰撞，碰后小球向右摆动的最大高度为
