��Ŀ����
����Ŀ����ͼ��ʾABΪ�뾶R=1m�ķ�֮һ�⻬��Ե��ֱԲ����������ķ�֮һԲ�������ڴ�����E=1��106V/m��ֱ���ϵ���ǿ�糡����һ����m=1kg��������q=1.4��10��5C����ɵ����壨����Ϊ�ʵ㣩����A������Ϸ�����A��H���ɾ�ֹ��ʼ�������䣨���ƿ�����������BC��Ϊ��L=2m�������嶯Ħ�����ئ�=0.2�Ĵֲھ�Եˮƽ�棬CD��Ϊ��Ǧ�=53���������DE��h=0.8m��б�森��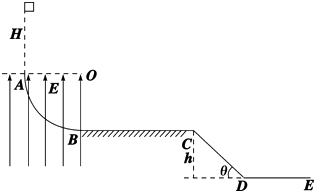
��1����H=1m���������ع��AB������͵㣬��������B��ʱ�Թ����ѹ����С��
��2��ͨ����ļ����жϣ��Ƿ����ijһHֵ����ʹ�����ع��AB������͵�B������ͣ�ھ���B��0.8m����
��3�����߶�H���㣺0.85m��H��1m����ͨ�������ʾ�������C�������ķ�Χ������֪sin53��=0.8��cos53��=0.6������Ҫ������̣���Ҫ�����λ�ã�����������ķ����Ժ���������
���𰸡�
��1��
�⣺�����ɾ�ֹ�˶���B��Ĺ����У����ݶ��ܶ����ã�
![]() ��
��
����B���Ժ���֧�������������糡���ĺ����ṩ���������У� ![]() ��
��
�������ݣ�������ʽ���FN=8N��
����ţ�ٵ������ɣ�֧������ѹ����С��ȣ������෴����������Թ����ѹ��Ϊ8N��������ֱ����
��2��
�⣺Ҫʹ�����ع��AB������͵�B����֧����Ϊ��ʱ����͵��и��ٶ�v��
![]() ��
��
�������ݽ��v=2m/s��
�ڴֲ�ˮƽ���ϵļ��ٶȴ�Сa=��g=2m/s2��
��������ֹͣ��λ�þ���B�ľ���x= ![]() ��
��
�����������Ź����A���˶���B�㣬ͣ��λ�������B��1m�����Բ�����������Hֵ
��3��
�⣺�ڻ��еĹ����У����ٶȽ�С��ƽ�������CDб���ϣ����ٶȽϴ�ʱ��ƽ�������DEƽ���ϣ�
��H=0.85mʱ��С������䵽����C��Ĺ��̣����ݶ��ܶ����ã�
mg��R+H����qER����mgL= ![]() mvC2��
mvC2��
���vC=1m/s��
����С����vC=1m/s��C���׳�ʱ����CDб���ϵ�P�㣬
����tan��= ![]() ��
��
sy= ![]() gt2��
gt2��
sx=vCt��
�ɼ��ι�ϵ������׳��������ľ���Ϊ ![]() m��CD�ľ���Ϊ1m��
m��CD�ľ���Ϊ1m��
���Լ����������P��D�ľ���Ϊ ![]() m��
m��
��H=1mʱ��С������䵽����C��Ĺ��̣����ݶ��ܶ����ã�
mg��R+H����qER����mgL= ![]() mvC��2��
mvC��2��
���vC��=2m/s��
����С����vC��=2m/s��C���׳�ʱ����ƽ��DE��Q�㣬
����ƽ���˶���ʽ�ɵã�
h= ![]() gt��2��
gt��2��
sx��=vC��t�䣬
���sx��=0.8m��
�ɼ��ι�ϵ�����CD��ˮƽ����Ϊ0.6m��
����DQ=0.2m��
���Դķ�ΧΪ��
��б���Ͼ���D�� ![]() m��Χ�ڣ�����ͼPD֮������
m��Χ�ڣ�����ͼPD֮������
��ˮƽ���Ͼ���D��0.2m��Χ�ڣ���ͼDQ֮������

����������1�����ݶ��ܶ���������嵽��B����ٶȣ����ţ�ٵڶ��������֧�����Ĵ�С���Ӷ����ţ�ٵ������ɵó�����B��Թ����ѹ������2������B����鲻����������С�ٶȣ����ţ�ٵڶ����ɺ��˶�ѧ��ʽ���ֹͣ��λ�þ���B�����С���룬�Ӷ������жϣ���3�����ݶ��ܶ����������C����ٶȣ����ƽ���˶�������������ķ�Χ��
�����㾫����������Ĺؼ����������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�����֪ʶ�������ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ���Լ��������������⣬�˽�����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������