题目内容
在2014年索契冬奥会跳台滑雪男子个人大跳台决赛中,波兰选手施托赫夺得冠军。跳台滑雪过程可简化如下。如图所示,abcde为同一竖直平面内的滑道,其中ab段和de段的倾角均为q=37°,ab段长L1 =110m,bc段水平其长度L2=27m(图中未标出),cd段竖直,其高度H=20m,de段足够长。设滑板与滑道之间的摩擦力为它们间压力的k倍(k=0.4,不考虑转弯b处的摩擦),运动员连同滑板的总质量m = 60kg。运动员从a点由静止开始下滑至c点水平飞出,在de上着地,再沿斜面方向下滑到安全区。运动员连同滑板整体可视为质点,忽略空气阻力,g取l0 m/s2,sin37?=0.6,cos37?=0.8。求:
(1)运动员从c点水平飞出时的速度大小v0;
(2)运动员在de着地时,沿斜面方向的速度大小v;
:(1) 20m/s (2)40m/s
解析试题分析:(1)运动员从a点到c点的过程中重力做功为 ,克服摩擦力做功为
,克服摩擦力做功为 ,根据动能定理得:
,根据动能定理得:
由以上各式并代入数据,解得
(2)运动员从c点水平飞出到落到de轨道上的过程中做平抛运动,设从c点到着陆点经过的时间为t,则:
水平位移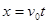 竖直位移
竖直位移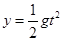
水平方向分速度 竖直方向分速度
竖直方向分速度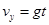
由几何关系得: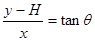
沿斜面方向和垂直斜面方向建立直角坐标系,将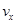 、
、 进行正交分解,于是可得:
进行正交分解,于是可得: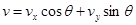 联立以上各式并代入数据,解得
联立以上各式并代入数据,解得
考点:本题考查动能定理、摩擦力做功、运动的合成与分解及平抛运动的规律,意在考查考生的理解能力、逻辑推理能力和综合应用能力。

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
下列说法正确的是
| A.力很大,位移也很大,这个力做的功可能为零 |
| B.一对作用力与反作用力对相互作用的系统做功之和一定为零 |
| C.静摩擦力对物体一定不做功,滑动摩擦力对物体一定做负功 |
| D.重力势能与参考面的选择有关,重力势能的变化量与参考面的选择无关 |
物体在合外力作用下做直线运动的v-t图象如图所示。下列表述正确的是
| A.在0—1 s内,合外力做正功 |
| B.在0—2 s内,合外力总是做负功 |
| C.在1—3 s内,合外力做负功 |
| D.在0—3 s内,合外力总是做正功 |
 C的正电荷从A点移动到B点, 电场力做了
C的正电荷从A点移动到B点, 电场力做了 J的负功。则A和B之间的电势差
J的负功。则A和B之间的电势差 = V。
= V。 ,下端A与上端B之间的长度L=20m,传送带以v=8m/s的速度顺时针转动。将质量m=4kg的小物体轻放在传送带下端A处,物块与传送带之间的动摩擦因数μ=5/4。取地球表面重力加速度g= l0m/s
,下端A与上端B之间的长度L=20m,传送带以v=8m/s的速度顺时针转动。将质量m=4kg的小物体轻放在传送带下端A处,物块与传送带之间的动摩擦因数μ=5/4。取地球表面重力加速度g= l0m/s ,sinθ=0.6,cosθ=0.8,求:物块从A到B的过程中,传送带对物块做的功。
,sinθ=0.6,cosθ=0.8,求:物块从A到B的过程中,传送带对物块做的功。
 。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求:
。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求: