题目内容
如图,间距为L的平行金属导轨上有一电阻为r的金属棒ab与导轨接触良好.导轨一端连接电阻R,其它电阻不计,磁感应强度为B,金属棒ab以速度v向右作匀速运动,则( )
| A.回路中电流为逆时针方向 |
| B.电阻R两端的电压为BLv |
| C.ab棒受到的安培力的方向向右 |
D.ab棒中电流大小为 |
A
解析试题分析:金属棒ab以速度v向右作匀速运动,由右手定则判定感应电流的方向由b→a,回路中电流为逆时针方向,再由左手定则判定出安培力的方向向左, A选项正确,C选项错误;利用导线切割式电动势公式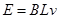 和闭合欧姆定律
和闭合欧姆定律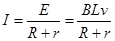 ,可求解ab两端的电压
,可求解ab两端的电压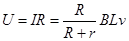 ,故B、D选项错误。
,故B、D选项错误。
考点:左手定则和右手定则 导体切割磁感线时的感应电动势

一足够长的铜管竖直放置,将一截面与铜管的内截面相同、质量为m的永久磁铁块由管上端口放人管内,不考虑磁铁与铜管间的摩擦,磁铁的运动速度可能是( )
| A.逐渐增大到定值后保持不变 |
| B.逐渐增大到一定值时又开始碱小.然后又越来越大 |
| C.逐渐增大到一定值时又开始减小,到一定值后保持不变 |
| D.逐渐增大到一定值时又开始减小到一定值之后在一定区间变动 |
如图4所示,金属杆ab以恒定的速率v在光滑平行导轨上向右滑行.设整个电路中总电阻为R(恒定不变),整个装置置于垂直纸面向里的匀强磁场中,下列叙述正确的是()
| A.ab杆中的电流与速率v成正比 |
| B.磁场作用于ab杆的安培力与速率v成正比 |
| C.电阻R上产生的电热功率与速率v的平方成正比 |
| D.外力对ab杆做功的功率与速率v的平方成正比 |
如图,金属棒ab、cd与足够长的水平光滑金属导轨垂直且接触良好,匀强磁场竖直向下.ab棒在恒力F作用下向右运动的过程中,有
|
C.abdca回路的磁通量先增加后减少
D.F做的功等于回路产生的总热量和系统动能增量之和
如图所示,在匀强磁场B中放一电阻不计的平行金属导轨,导轨跟固定的大导体矩形环M相连接,导轨上放一根金属导体棒ab并与导轨紧密接触,磁感线垂直于导轨所在平面.若导体棒匀速地向右做切割磁感线的运动,则在此过程中M所包围的固定闭合小矩形导体环N中电流表内( )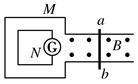
| A.有自下而上的恒定电流 |
| B.产生自上而下的恒定电流 |
| C.电流方向周期性变化 |
| D.没有感应电流 |
如图甲所示,两根电阻忽略不计的导轨平行放置,导轨左端接电阻R1,右端接小灯泡L,导体棒AB垂直于导轨放置,电阻R1、导体棒AB和小灯泡L的电阻均为R(不计灯泡电阻随温度的变化),虚线MN右侧有垂直导轨平面的磁场,当导体棒AB从MN左侧某处匀速向右运动时开始计时,磁感应强度随时间变化如图乙所示,若导体棒AB从开始运动到穿越磁场的过程中,灯泡的亮度始终不变,则导体棒AB在穿越磁场前后电阻R1上消耗的功率之比是( )

| A.1∶1 | B.1∶2 | C.1∶3 | D.1∶4 |
如图所示,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且接触良好,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,ab棒的速度大小为v,则ab棒在这一过程中( ).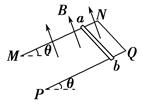
A.运动的平均速度大小为 v v |
B.下滑的位移大小为 |
| C.产生的焦耳热为qBLv |
D.受到的最大安培力大小为 sin θ sin θ |
如图所示是测量通电螺线管内部磁感应强度的一种装置:把一个很小的测量线圈放在待测处(测量线圈平面与螺线管轴线垂直),将线圈与可以测量电荷量的冲击电流计G串联,当将双刀双掷开关K由位置1拨到位置2时,测得通过测量线圈的电荷量为q。已知测量线圈的匝数为N,截面积为S,测量线圈和G串联回路的总电阻为R。下列判断正确的是:
A.在此过程中,穿过测量线圈的磁通量的变化量 |
B.在此过程中,穿过测量线圈的磁通量的变化量 |
C.待测处的磁感应强度的大小为 |
D.待测处的磁感应强度的大小为 |
