题目内容
6. 如图所示,坐标系xOy在竖直平面内,x轴沿水平方向.x>0的区域有垂直于坐标平面向外的匀强磁场,磁感应强度大小为B1;第三象限同时存在着垂直于坐标平面向外的匀强磁场和竖直向上的匀强电场,磁感应强度大小为B2,电场强度大小为E.x>0的区域固定一与x轴成θ=30°角的绝缘细杆.一个带电小球a穿在细杆上匀速下滑过N点进入第三象限,在第三象限内做匀速圆周运动且垂直经过x轴上的Q点.已知Q点到坐标原点O的距离为$\frac{3}{2}$l,重力加速度为g,B1=7E$\sqrt{\frac{1}{10π•g•l}}$,B2=E$\sqrt{\frac{5π}{6gl}}$,.空气阻力忽略不计,求:
如图所示,坐标系xOy在竖直平面内,x轴沿水平方向.x>0的区域有垂直于坐标平面向外的匀强磁场,磁感应强度大小为B1;第三象限同时存在着垂直于坐标平面向外的匀强磁场和竖直向上的匀强电场,磁感应强度大小为B2,电场强度大小为E.x>0的区域固定一与x轴成θ=30°角的绝缘细杆.一个带电小球a穿在细杆上匀速下滑过N点进入第三象限,在第三象限内做匀速圆周运动且垂直经过x轴上的Q点.已知Q点到坐标原点O的距离为$\frac{3}{2}$l,重力加速度为g,B1=7E$\sqrt{\frac{1}{10π•g•l}}$,B2=E$\sqrt{\frac{5π}{6gl}}$,.空气阻力忽略不计,求:(1)带电小球a的电性及其比荷$\frac{q}{m}$;
(2)带电小球a与绝缘细杆的动摩擦因数μ;
(3)当带电小球a刚离开N点时,从y轴正半轴距原点O为h=$\frac{20πl}{3}$的P点(图中未画出)以某一初速度平抛一个不带电的绝缘小球b,b球刚好运动到x轴与向上运动的a球相碰,则b球的初速度为多大?
分析 (1)粒子在第3象限做匀速圆周运动,重力和电场力平衡,洛伦兹力提供向心力,根据平衡条件求解电场强度;
(2)带电小球在第3象限做匀速圆周运动,画出轨迹,结合几何关系得到半径,然后结合牛顿第二定律求解速度;带电小球a穿在细杆上匀速下滑,受重力、支持力和洛伦兹力,三力平衡,根据共点力平衡条件并结合合成法列式求解;
(3)绝缘小球b做平抛运动,根据平抛运动的分运动公式求解运动到x轴的时间;小球a在第3象限做圆周运动,第2象限做竖直上抛运动,分阶段求解出其经过x轴的时间,然后根据等时性列式.
解答 解:(1)由带电小球在第三象限内做匀速圆周运动可得:带电小球带正电
且mg=qE,
解得:$\frac{q}{m}=\frac{g}{E}$.
(2)带电小球从N点运动到Q点的过程中,有:$qv{B}_{2}=m\frac{{v}^{2}}{R}$,
由几何关系有:$R+Rsinθ=\frac{3}{2}l$,
联立解得:$v=\sqrt{\frac{5πgl}{6}}$.
带电小球在杆上匀速时,由平衡条件有:mgsinθ=μ(qvB1-mgcosθ),
解得:$μ=\frac{\sqrt{3}}{4}$.
(3)带电小球在第三象限内做匀速圆周运动的周期:T=$\frac{2πR}{v}$=$\sqrt{\frac{24πl}{5g}}$,
带电小球第一次在第二象限竖直上下运动的总时间为:${t}_{0}=\frac{2v}{g}=\sqrt{\frac{10πl}{3g}}$.
绝缘小球b平抛运动至x轴上的时间为:$t=\sqrt{\frac{2h}{g}}=2\sqrt{\frac{10πl}{3g}}$,
两球相碰有:t=$\frac{T}{3}+n({t}_{0}+\frac{T}{2})$,
联解得:n=1
设绝缘小球b平抛的初速度为v0,则:$\frac{7}{2}l={v}_{0}t$,
解得:${v}_{0}=\sqrt{\frac{147gl}{160π}}$.
答:(1)带电小球a的电性及其比荷$\frac{q}{m}$为$\frac{g}{E}$;
(2)带电小球a与绝缘细杆的动摩擦因数为$\frac{\sqrt{3}}{4}$;
(3)b球的初速度为$\sqrt{\frac{147gl}{160π}}$.
点评 本题多物体、多过程、多规律,是典型的三多问题;关键是明确两个小球的运动规律,然后分阶段根据牛顿第二定律、平衡条件、运动学公式、平抛运动的分运动公式列式求解,较难.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案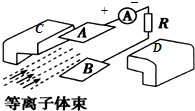 如图为磁流体发电机的原理图,等离子体束(含有正、负离子)以某一速度垂直喷射入由一对磁极CD产生的匀强磁场中,A、B是一对平行于磁场放置的金属板.稳定后电流表中的电流从“+”极流向“-”极,由此可知( )
如图为磁流体发电机的原理图,等离子体束(含有正、负离子)以某一速度垂直喷射入由一对磁极CD产生的匀强磁场中,A、B是一对平行于磁场放置的金属板.稳定后电流表中的电流从“+”极流向“-”极,由此可知( )| A. | D磁极为N极 | |
| B. | 正离子向A板偏转 | |
| C. | 负离子向D磁极偏转 | |
| D. | 离子在磁场中偏转过程洛仑兹力对其不做功 |
 2012年4月16日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每378天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )
2012年4月16日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,二者几乎成一条直线.该天象每378天发生一次,土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆,根据我们日常生活知识可知( )| A. | 土星公转的速率比地球大 | |
| B. | 土星公转的向心加速度比地球小 | |
| C. | 土星公转的周期约为1.1×104天 | |
| D. | 假如土星适度加速,有可能与地球实现对接 |
| A. | 0.4m/s2 | B. | 0.37m/s2 | C. | 2.6m/s2 | D. | 0.43m/s2 |
| A. | 轨道半径增大,机械能增大 | B. | 卫星动能增大,引力势能增大 | ||
| C. | 轨道半径减小,机械能减小 | D. | 卫星动能减小,引力势能增大 |
| A. | 汤姆生通过对阴极射线的研究发现了电子 | |
| B. | 卢瑟福通过对α粒子散射实验的研究发现了质子 | |
| C. | 贝克勒尔通过对天然放射现象的研究发现了原子的核式结构 | |
| D. | 查德威克发现了中子并测出了中子的质量 |
 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )| A. | 小球仍在水平面内做匀速圆周运动 | |
| B. | 在绳b被烧断瞬间,a绳中张力突然增大 | |
| C. | 在绳b被烧断瞬间,小球的向心加速度不变 | |
| D. | 若角速度ω较大,小球可能在垂直于平面ABC的竖直平面内做圆周运动 |
| A. | 损失的电功率与输送电线上电压降成正比 | |
| B. | 损失的电功率与输送电压成正比 | |
| C. | 损失的电功率与输送电线上电压降的平方成正比 | |
| D. | 损失的电功率与输送电压的平方成正比 |
