Question

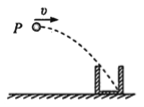
【题目】如图所示，长s=5m、倾角θ=37°的斜面各通过一小段光滑圆弧与水平传送带和水平地面平滑连接，传送带长L=1.6m，以恒定速率v0=4m/s逆时针运行，将一可看作质点的物块轻轻地放上传送带右端A，物块滑到传送带左端B时恰好与传送带共速并沿斜面下滑，已知物块和传送带、斜面、水平地面间的动摩擦因数都为μ，物块最终静止在水平面上的D点，取g=10m/s2，求：

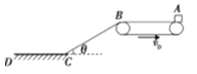
（1）动摩擦因数μ的值．

（2）水平面上CD的长．

（3）物块从A到D所经历的时间．

Answer 1

【答案】（1）0.5 （2）3.6m （3）3s

【解析】试题分析：（1）传送带上由速度位移公式可得

有牛顿第二定律得

可以得到：

（2）从B到D由动能定理得

解得：x="3.6m"

（3）在传送带上加速度为

到达传送带左端所需时间为

在斜面上产生的加速度为

下滑到斜面底端

解得

下滑到斜面的速度为

在水平地面上运动的时间为

故所需时间为