题目内容
磁场具有能量，磁场中单位体积所具有的能量叫做能量密度，其值为
，式中B是磁感强度，μ是磁导率，在空气中μ为一已知常数．为了近似测得条形磁铁磁极端面附近的磁感强度B，一学生用一根端面面积为A的条形磁铁吸住一相同面积的铁片P，再用力将铁片与磁铁拉开一段微小距离△l，并测出拉力F，如图所示．因为F所作的功等于间隙中磁场的能量，所以由此可得磁感强度B与F、A之间的关系为B= ．
【答案】分析：由于拉力F所作的功等于间隙中磁场的能量，能量密度为磁场中单位体积所具有的能量，故用能量除以体积就可以列出关系式求出磁感强度B与F、A之间的关系．
解答：解：由题意，磁场中单位体积所具有的能量叫做能量密度，其值为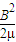
条形磁铁与铁片P之间的磁场具有的能量等于拉力F做的功，故
E=F?△x ①
量密度为磁场中单位体积所具有的能量，故
=
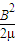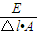②
由①②可解得
B=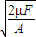
故答案为：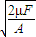
．
点评：本题关键根据题意得到磁场能量密度的定义，然后根据功能关系求得条形磁铁与铁片P之间的磁场所具有的能量，再根据题意列式求解．
解答：解：由题意，磁场中单位体积所具有的能量叫做能量密度，其值为
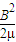
条形磁铁与铁片P之间的磁场具有的能量等于拉力F做的功，故
E=F?△x ①
量密度为磁场中单位体积所具有的能量，故
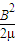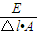= ②由①②可解得
B=
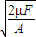
故答案为：
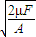．点评：本题关键根据题意得到磁场能量密度的定义，然后根据功能关系求得条形磁铁与铁片P之间的磁场所具有的能量，再根据题意列式求解．
练习册系列答案
相关题目
磁场具有能量，磁场中单位体积所具有的能量叫做能量密度，其值为B2/2μ，式中B是磁感应强度，“μ是磁导率，在空气中μ为一已知常数．为了近似测得条形磁铁磁极端面附近的磁感应强度B，一学生用一根端面面积为A的条形磁铁吸住一相同面积的铁片P，再用力将铁片与磁铁拉开一段微小距离△l，并测出拉力F，如图所示．因为F所做的功等于间隙中磁场的能量，所以由此可得磁感应强度B与F、A之间的关系为B=
（2002?上海）磁场具有能量，磁场中单位体积所具有的能量叫做能量密度，其值为
，式中B是磁感应强度，μ是磁导率，在空气中μ为一已知常数，为了近似测得条形磁铁磁极两端面附近的磁感应强度B，一个学生用一根端面面积为S的条形磁铁吸住一相同面积的铁片P，再用力将铁片与磁铁拉开一段微小距离ΔL，并测出拉力F，如图1所示.因为F所做的功等于间隙中磁场的能量，所以由此可测得磁感应强度B与F、S之间的关系为B=_____________.
，式中B是磁感应强度，μ是磁导率，在空气中μ为一已知常数.为了近似测得条形磁铁磁极端面附近的磁感应强度B，一学生用一根端面面积为A的条形磁铁吸住一相同面积的铁片P，再用力将铁片与磁铁拉开一段微小距离Δl，并测出拉力F，如图
.式中B是磁感应强度，μ是磁导率，在空气中μ为一已知常数.为了近似测得条形磁铁磁极端面附近的磁感应强度B,一学生用一根端面面积为A的条形磁铁吸住一相同面积的铁片P,再用力将铁片与磁铁拉开一段微小距离Δl,并测出拉力F,如图