题目内容
如图所示，有两个带正电的粒子P和Q同时从匀强磁场的边界上的M点分别以30°和60°（与边界的交角）射入磁场，又同时从磁场边界上的同一点N飞出，设边界上方的磁场范围足够大，不计粒子所受的重力影响，则两粒子在磁场中的半径之比rp：rQ=| 3 |
| 3 |
4 2 |
质子
质子
，理由是质量数与电荷数之比为1：1
质量数与电荷数之比为1：1
．分析：带有正电荷的A粒子和B粒子同时从O点不同角度射入匀强磁场后，从Q点飞出．由粒子的电性可确定洛伦兹力方向，根据处理规律：定圆心、画圆弧、求半径．并根据几何关系可确定粒子的半径关系，根据运动时间相等及周期公式求解荷质比，根据半径公式求解速度比．
解答：解：（1）粒子运动的轨迹如图，
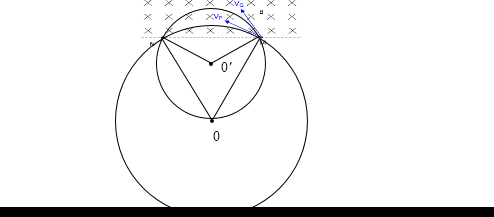
粒子P的轨迹是以O为圆心的圆，∠MON=180°-2（90°-30°）=60°所以△MON是等边三角形，rP=
；
粒子Q的轨迹是以O′为圆心的圆，∠MO′N=180°-2（90°-60°）=120°，所以rQ=
=
；
所以：
=
（2）带电粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，即：qvB=
，又：T=
．所以得：T=
粒子在磁场中运动的时间与偏转角之间的关系：
=
两种粒子在磁场中运动的时间相等，所以：
?
=
?
整理得：
=2
，所以P粒子的质量数与电荷数之比为1：1，P粒子可能是质子．
故答案为：（1）
=
（2）质子，质量数与电荷数之比为1：1
粒子P的轨迹是以O为圆心的圆，∠MON=180°-2（90°-30°）=60°所以△MON是等边三角形，rP=
. |
| MN |
粒子Q的轨迹是以O′为圆心的圆，∠MO′N=180°-2（90°-60°）=120°，所以rQ=
| ||||
| cos30° |
| ||
| 3 |
. |
| MN |
所以：
| rP |
| rQ |
| 3 |
（2）带电粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，即：qvB=
| mv2 |
| r |
| 2πr |
| v |
| 2πm |
| qB |
粒子在磁场中运动的时间与偏转角之间的关系：
| t |
| T |
| θ |
| 2π |
两种粒子在磁场中运动的时间相等，所以：
| ∠MON |
| 2π |
| 2π?mp |
| qpB |
| ∠MO′N |
| 2π |
| 2π?mQ |
| qQB |
整理得：
| mQ |
| mP |
| qP |
故答案为：（1）
| rP |
| rQ |
| 3 |
（2）质子，质量数与电荷数之比为1：1
点评：利用圆弧的特性来确定圆心，画出圆弧并运用几何关系来算出圆弧的半径，同时还体现出控制变量的思想．
练习册系列答案
相关题目
如图所示，有两个完全相同的金属球A、B，B固定在绝缘地板上，A在离B高H的正上方，由静止释放，与B发生碰撞后回跳高度为h，设碰撞过程中无动能损失，空气阻力不计．（ ）
