题目内容
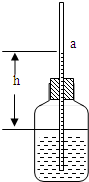 已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a上升到一定的高度.将玻璃瓶放置在地面上,记录下此时管内水面a的位置,再将玻璃瓶放到离地1.2米的讲台上时,则玻璃管内水面将上升
已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a上升到一定的高度.将玻璃瓶放置在地面上,记录下此时管内水面a的位置,再将玻璃瓶放到离地1.2米的讲台上时,则玻璃管内水面将上升分析:根据毛细管中高度差产生的压强加上大气压等于瓶中气体的压强列式计算;
先根据毛细管中高度差产生的压强加上大气压等于瓶中气体的压强列式计算出瓶内气压,然后根据理想气体状态方程列式求解出到达B处后的瓶内压强,最后得到B处的大气压强,并计算高度差.
先根据毛细管中高度差产生的压强加上大气压等于瓶中气体的压强列式计算出瓶内气压,然后根据理想气体状态方程列式求解出到达B处后的瓶内压强,最后得到B处的大气压强,并计算高度差.
解答:解:玻璃瓶放到离地1.2m的讲台上时,大气压降低了0.1mmHg,毛细管中水面上升0.1mm×13.6=1.36mm;
大气压为750mmHg,在A处时,
瓶内气体压强为:P1=750mmHg+
mmHg=765mmHg;
根据理想气体状态方程,有
=
,
代入数据得到:
=
,
解得P2=767.55mmHg;
故B处大气压为PB=P2-Ph=767.55mmhg-
=749.55mmHg;
故A、B间的高度差为:△h=(750-749.55)×12=5.4m;
故答案为:1.36;5.4.
大气压为750mmHg,在A处时,
瓶内气体压强为:P1=750mmHg+
| 204 |
| 13.6 |
根据理想气体状态方程,有
| P1V1 |
| T1 |
| P2V2 |
| T2 |
代入数据得到:
| 765×V |
| 300 |
| P2V |
| 301 |
解得P2=767.55mmHg;
故B处大气压为PB=P2-Ph=767.55mmhg-
| (204+40.8)mmHg |
| 13.6 |
故A、B间的高度差为:△h=(750-749.55)×12=5.4m;
故答案为:1.36;5.4.
点评:本题关键对高处瓶内水平面的液柱受力分析得到大气压强和瓶内气压的关系式,然后结合理想气体状态方程列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?崇明县二模)已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差.
(2012?崇明县二模)已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差. 已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103Kg/m3)
已知地面附近高度每升高12m,大气压降低1mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103Kg/m3) m,大气压降低
m,大气压降低 mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103kg/m3)
mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103kg/m3)
 m的讲台上时,则玻璃管内水面将 (上升,下降) mm;(设温度保持不变)
m的讲台上时,则玻璃管内水面将 (上升,下降) mm;(设温度保持不变) mmHg的A处,测得水柱的高度
mmHg的A处,测得水柱的高度 mm.然后将装置缓慢地平移另一高度的B处,待稳定后发现水柱升高了
mm.然后将装置缓慢地平移另一高度的B处,待稳定后发现水柱升高了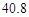 mm,已知B处比A处的温度高1℃,则AB间高度差为 m;
mm,已知B处比A处的温度高1℃,则AB间高度差为 m;  m,大气压降低
m,大气压降低 mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103kg/m3)
mmHg.为了观测大气压这一微小变化,某实验小组巧妙地设计了如图所示的一个实验,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内有一定的高度差.(不计水面升降引起的瓶内空气体积的变化,水银的密度为13.6×103kg/m3)
 m的讲台上时,则玻璃管内水面将 (上升,下降) mm;(设温度保持不变)
m的讲台上时,则玻璃管内水面将 (上升,下降) mm;(设温度保持不变) mmHg的A处,测得水柱的高度
mmHg的A处,测得水柱的高度 mm.然后将装置缓慢地平移另一高度的B处,待稳定后发现水柱升高了
mm.然后将装置缓慢地平移另一高度的B处,待稳定后发现水柱升高了 mm,已知B处比A处的温度高1℃,则AB间高度差为 m;
mm,已知B处比A处的温度高1℃,则AB间高度差为 m;