题目内容
 (2013?静安区一模)如图,在斜面顶端先后水平抛出同一小球,第一次小球落到斜面中点,第二次小球落到斜面底端.则两次小球运动时间之比t1:t2=_
(2013?静安区一模)如图,在斜面顶端先后水平抛出同一小球,第一次小球落到斜面中点,第二次小球落到斜面底端.则两次小球运动时间之比t1:t2=_1:
| 2 |
1:
;两次小球落到斜面上时动能之比EK1:EK2=| 2 |
1:2
1:2
.分析:小球落在斜面上,竖直方向上的位移和水平方向上的位移的比值是一定值,知运动的时间与初速度有关.从而求出时间比.
求出末速度,根据动能的表达式即可球动能之比.
求出末速度,根据动能的表达式即可球动能之比.
解答:解:在斜面顶端先后水平抛出同一小球,第一次小球落到斜面中点,第二次小球落到斜面底端.所以两次竖直方向下落的高度之比为:1:2;
根据t=
可知,则两次小球运动时间之比t1:t2=1:
因为水平位移之比是1:2,则水平速度之比为1:
设斜面倾角为θ,则落地时有:v=
所以落地时动能为:
m(
)2,所以动能之比为初速度的平方比,即为1:2
故答案为:1:
;1:2
根据t=
|
| 2 |
因为水平位移之比是1:2,则水平速度之比为1:
| 2 |
设斜面倾角为θ,则落地时有:v=
| v0 |
| cosθ |
所以落地时动能为:
| 1 |
| 2 |
| v0 |
| cosθ |
故答案为:1:
| 2 |
点评:解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.以及知道小球落在斜面上,竖直方向上的位移和水平方向上的位移比值一定.

练习册系列答案
相关题目
 (2013?静安区一模)如图所示,木块质量m=1.04kg,在与水平方向成θ=37°角、斜向右上方的恒定拉力F作用下,以a=2.0m/s2的加速度从静止开始做匀加速直线运动,在3s末时撤去拉力F.已知木块与地面间的动摩擦因数μ=0.4,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(2013?静安区一模)如图所示,木块质量m=1.04kg,在与水平方向成θ=37°角、斜向右上方的恒定拉力F作用下,以a=2.0m/s2的加速度从静止开始做匀加速直线运动,在3s末时撤去拉力F.已知木块与地面间的动摩擦因数μ=0.4,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求: (2013?静安区一模)一定质量的理想气体,从图示A状态开始,经历了B、C,最后到D状态,下列判断中正确的是( )
(2013?静安区一模)一定质量的理想气体,从图示A状态开始,经历了B、C,最后到D状态,下列判断中正确的是( )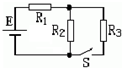 (2013?静安区一模)图中电阻R1、R2、R3的阻值相等,电池的内阻不计.开关S接通前流过R2的电流为I2,接通后流过R2的电流为I2',则I2:I2'为( )
(2013?静安区一模)图中电阻R1、R2、R3的阻值相等,电池的内阻不计.开关S接通前流过R2的电流为I2,接通后流过R2的电流为I2',则I2:I2'为( )