题目内容
【题目】如图所示,质量mA=1.0kg的物块A放在水平固定桌面上,由跨过光滑小定滑轮的轻绳与质量mB=1.5kg的物块B相连.轻绳拉直时用手托住物块B,使其静止在距地面h=0.6m的高度处,此时物块A与定滑轮相距L.已知物块A与桌面间的动摩擦因数μ=0.25,g取10m/s2 . 现释放物块B,物块B向下运动.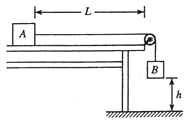
(1)求物块B着地前加速度的大小及轻绳对它拉力的大小.
(2)设物块B着地后立即停止运动,要求物块A不撞到定滑轮,则L至少多长?
【答案】
(1)解:设加速度大小为a,轻绳对B拉力的大小为F,根据牛顿第二定律 有
对A:F﹣μmAg=mAa ①
对B:mBg﹣F=mBa ②
①②联立代入数据得:a=5m/s2③
F=7.5N
答:求物块B着地前加速度的大小为5m/s2,轻绳对它拉力的大小为7.5N
(2)解:设物块B着地前的速率为v,根据运动学公式v2=2ax 有
对A:v2=2ah ④
块B着地后,对B由牛顿第二定律得:μmAg=mAa′⑤
根据运动学公式 ![]() 得:
得:
0﹣v2=2(﹣a′)x ⑥
③④⑤⑥联立解得x=1.2m h=0.6m
由题意知:L≥h+x=1.2+0.6m=1.8m
所以,L至少1.8m
答:股物块B着地后立即停止运动,要求物块A不撞到定滑轮,则L至少为1.8m
【解析】(1)分别以物块A和B受力分析,利用牛顿第二定律列式求解;(2)物块先做匀加速运动,物块B碰地后,A开始做匀减速运动,到达滑轮时速度恰好为零,则L最小.

练习册系列答案
相关题目