Question

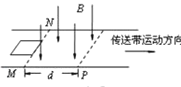
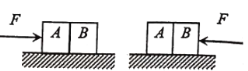
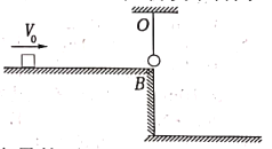
【题目】如图所示，质量为1kg的物块放在水平平台上的A点，平台离地面的高度为0.8m，物块离平台右端B点距离为1.2m，一个质量为0.5kg的小球用轻绳悬吊在天花板上的O点，O点在B点正上方lm处，小球与平台刚好要接触，给物块一个向右、大小为2m/s的初速度，物块滑到B点与悬挂的小球相碰，物块的落地点离B点的水平距离为0.8m，已知物块平台间的动摩擦因数为0.5，重力加速度g=10m/s2，不计小球的大小，求:

(1)物块与小球相碰前的速度大小;

(2)小球被碰后一瞬间细绳上的拉力。

Answer 1

【答案】(1) 4m/s (2) 13N

【解析】

(1) 设物块A与小球相碰前的速度大小为v1，根据动能定理有

求得

v 1=4m/s

(2)物块与小球相碰后物块做平抛运动，设物块做平抛运动的初速度大小为v2，则：

x=v2t

求得：

t=0.4s，v2 = 2m/s

设小球被碰后速度大小为v3，根据动量守恒定律有：

求得：

设小球被碰后一瞬间轻绳的拉力为F， 根据牛顿第二定律有：

求得：

F=13N