题目内容
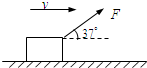
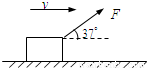
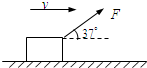 如图所示,商场工作人员用与水平方向成37°斜向上、大小为200N的力F拉着货物沿水平地面做匀速运动,货物的质量为52kg,速度大小为8m/s,某时刻撤去拉力后,货物滑行了一段距离停下(cos37°=0.8,sin37°=0.6).求:
如图所示,商场工作人员用与水平方向成37°斜向上、大小为200N的力F拉着货物沿水平地面做匀速运动,货物的质量为52kg,速度大小为8m/s,某时刻撤去拉力后,货物滑行了一段距离停下(cos37°=0.8,sin37°=0.6).求:(1)货物与水平面间动摩擦因数多大?
(2)撤去拉力后,货物还能运动多长时间?
(3)若将力F改为水平,使此货物从静止开始运动,则F至少做多少功,能使货物到达200m处的仓库.
分析:(1)根据货物在水平面上做匀速直线运动,抓住合力等于零求出动摩擦因数.
(2)撤去拉力后,根据牛顿第二定律求出加速度的大小,再根据匀变速直线运动的速度时间公式求出货物的运动时间.
(3)将货物从静止开始运动到200m处,临界情况是末速度为零,根据动能定理求出F至少做功的多少.
(2)撤去拉力后,根据牛顿第二定律求出加速度的大小,再根据匀变速直线运动的速度时间公式求出货物的运动时间.
(3)将货物从静止开始运动到200m处,临界情况是末速度为零,根据动能定理求出F至少做功的多少.
解答:解:(1)货物受重力、支持力、拉力摩擦力处于平衡,有:
Fcos37°=f
f=μ(mg-Fsin37°)
联立两式解得:μ=0.4.
(2)撤去拉力后,货物的加速度a=
=μg=4m/s2
则货物还能运动的时间t=
=2s.
(3)根据动能定理得:
WF-μmgx=0
解得WF=μmgx=0.4×520×200J=4.16×104J.
答:(1)货物与水平面间动摩擦因数为0.4.
(2)撤去拉力后,货物还能运动2s.
(3)F至少做4.16×104J功,能使货物到达200m处的仓库.
Fcos37°=f
f=μ(mg-Fsin37°)
联立两式解得:μ=0.4.
(2)撤去拉力后,货物的加速度a=
| μmg |
| m |
则货物还能运动的时间t=
| v |
| a |
(3)根据动能定理得:
WF-μmgx=0
解得WF=μmgx=0.4×520×200J=4.16×104J.
答:(1)货物与水平面间动摩擦因数为0.4.
(2)撤去拉力后,货物还能运动2s.
(3)F至少做4.16×104J功,能使货物到达200m处的仓库.
点评:本题综合运用了牛顿第二定律和动能定理以及运动学公式,关键是理清运动过程,选择合适的规律进行求解.

练习册系列答案
相关题目
 如图所示,电力工作人员在几百万伏的高压线上进行带电作业,电工全身穿戴带电作业用屏蔽服,屏蔽服是用导电金属材料与纺织纤维混纺交织成布后再做成的服装,下列说法正确的是( )
如图所示,电力工作人员在几百万伏的高压线上进行带电作业,电工全身穿戴带电作业用屏蔽服,屏蔽服是用导电金属材料与纺织纤维混纺交织成布后再做成的服装,下列说法正确的是( )